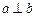题目内容
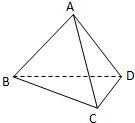
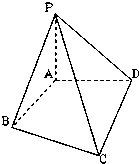
在如图所示的多面体中，底面△ABC是边长为2的正三角形，DA和EC均垂直于平面ABC，且DA=2，EC=1．
（Ⅰ）求点A到平面BDE的距离；
（Ⅱ）求二面角B-ED-A的正切值．
（Ⅰ）求点A到平面BDE的距离；
（Ⅱ）求二面角B-ED-A的正切值．
（Ⅰ）∵DE=BE=
，BD=2
，
∴S△BDE=
，设点A到平面BDE的距离为h．
又∵S△ABC=
，VB-ADE=VA-BDE
∴
•
•2=
•
•h∴h=
即点A到平面BDE的距离为
．…（6分）
（Ⅱ）∵DA⊥平面ABC，∴平面DACE⊥平面ABC
取AC的中点M，连接BM，则BM⊥AC，BM⊥平面DACE．
过M作MN⊥DE，交DE于N，连接BN，则BN⊥DE，∴∠BNM是所求二面角的平面角．
设AC、DE的延长线相交于点P，∵DA=2EC，∴CP=2由△MNP∽△DAP得
=
，
MP=3，DA=2，DP=2
，∴MN=
又∵BM=
，∴tan∠BNM=
．…（12分）
| 5 |
| 2 |
∴S△BDE=
| 6 |
又∵S△ABC=
| 3 |
∴
| 1 |
| 3 |
| 3 |
| 1 |
| 3 |
| 6 |
| 2 |
即点A到平面BDE的距离为
| 2 |
（Ⅱ）∵DA⊥平面ABC，∴平面DACE⊥平面ABC
取AC的中点M，连接BM，则BM⊥AC，BM⊥平面DACE．
过M作MN⊥DE，交DE于N，连接BN，则BN⊥DE，∴∠BNM是所求二面角的平面角．
设AC、DE的延长线相交于点P，∵DA=2EC，∴CP=2由△MNP∽△DAP得
| MN |
| MP |
| DA |
| DP |
MP=3，DA=2，DP=2
| 5 |
| 3 | ||
|
又∵BM=
| 3 |
| ||
| 3 |
练习册系列答案
相关题目
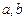为两条直线，
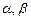为两个平面.下列四个命题中，正确的命题是 ( )
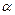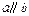
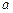
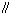
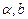
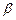
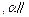
所成的角相等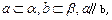，则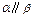
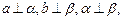则
则
