题目内容
已知数列{an}为等差数列,且a1+a7+a13=4π,则tana7=( )
A.
| B.-
| C.±
| D.-
|
∵数列{an}为等差数列,
∴a1+a13=2a7,又a1+a7+a13=4π,
∴3a7=4π,即a7=
,
则tana7=tan
=tan(π+
)=tan
=
.
故选A
∴a1+a13=2a7,又a1+a7+a13=4π,
∴3a7=4π,即a7=
| 4π |
| 3 |
则tana7=tan
| 4π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 3 |
故选A

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案
相关题目
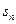 ,若
,若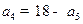 ,则
,则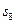 =
= 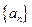 是公比为
是公比为 的等比数列,
的等比数列,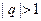 ,令
,令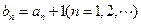 ,若数列
,若数列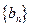 有连续四项在集合
有连续四项在集合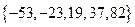 中,则
中,则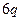 = ▲ .
= ▲ .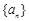 的公差
的公差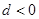 ,且
,且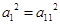 ,则数列
,则数列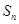 取最大值时
取最大值时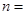 ( )
( )