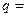题目内容
设函数f(x)=x3＋ax2＋bx＋c,且f(0)=0为函数的极值,则有
| A．c≠0 | B．b=0 |
| C．当a＞0时,f(0)为极大值 | D．当a＜0时,f(0)为极小值 |
B
本题考查函数的极值与导数的关系.
由f(0)=0,得c=0,排除A.
又f′(x)=3x2＋2ax＋b,因x=0处函数有极值,所以x=0是方程f′(x)=0的实根,可得b=0.
由f(0)=0,得c=0,排除A.
又f′(x)=3x2＋2ax＋b,因x=0处函数有极值,所以x=0是方程f′(x)=0的实根,可得b=0.
练习册系列答案
相关题目
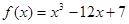在
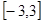上的最大值与最小值的差是
=
.
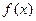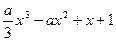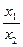≤5,求a的取值范围。12分
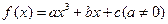为奇函数，导函数
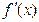的最小值为-12，函数
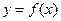的图象在点P
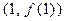处的切线与直线
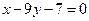垂直.(1)求a，b，c的值；(2)求
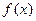的各个单调区间，并求
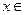[-1, 3]时的最大值和最小值.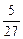
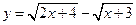的值域 
（
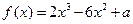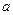是常数）在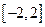
上有最大值3，那么它在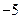
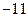
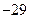
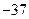
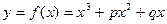的图象与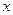
轴切于非原点的一点，且
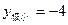，那么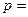
，