题目内容
已知函数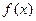
=
.
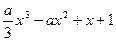（1）若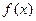在（－∞，+∞）上是增函数，求a的取值范围.
(2) 若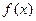在x=x1及x=x2 (x1, x2>0)处有极值，且1<
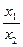≤5,求a的取值范围。12分
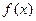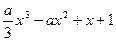=.（1）若
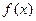在（－∞，+∞）上是增函数，求a的取值范围.(2) 若
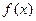在x=x1及x=x2 (x1, x2>0)处有极值，且1<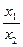≤5,求a的取值范围。12分(1) a的取值范围是0≤a≤1.(2) 1<a≤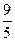
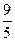
(1)∵
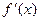=ax2－2ax+1……………………………...….1分
∴当a=0时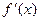，，=1>0,故结论成立………………………………2分
当a>0时,[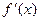]min=
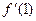=1－a≥0,∴a≤1即0<a≤1.…………..4分
当a<0时,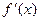在(0,+∞)上不恒大于或等于0，故舍去.…………..5分
综上得a的取值范围是0≤a≤1.
(2) 令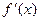=ax2－2ax+1=0，由题知其二根为x1，x2且x1+x2=2，x1x2=
…………..7分
∵1<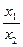≤5 ∴x1≤2－x2≤5x1 ∴
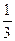≤x1<1 …………..9分
∴x1(2－x2)= ∴=－(x1－1)2+1…………..11分
∴
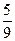≤<1 ∴1<a≤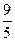…………..12分
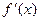=ax2－2ax+1……………………………...….1分∴当a=0时，，
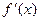=1>0,故结论成立………………………………2分当a>0时,[
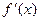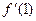]min==1－a≥0,∴a≤1即0<a≤1.…………..4分当a<0时,
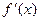在(0,+∞)上不恒大于或等于0，故舍去.…………..5分综上得a的取值范围是0≤a≤1.
(2) 令
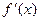=ax2－2ax+1=0，由题知其二根为x1，x2且x1+x2=2，x1x2=…………..7分∵1<
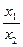≤5 ∴x1≤2－x2≤5x1 ∴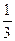≤x1<1 …………..9分∴x1(2－x2)=
∴=－(x1－1)2+1…………..11分∴
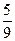≤<1 ∴1<a≤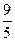…………..12分
练习册系列答案
阅读快车系列答案
相关题目
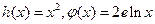（其中e为自然对数）
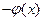的极值。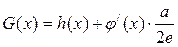
（常数a>0），当x>1时，求函数G(x)的单调区
. 
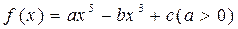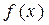在
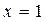和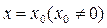
处有不同的极值，且极大值为4，
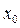及实数
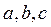的值；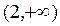
上单调递增且
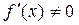，求
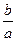的最大值.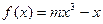 
的图象上以N（1，n）为切点的切线倾斜角为
.
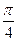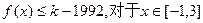恒成立？若存在，求出最小的正整数k，否则请说明理由.
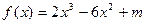（m为常数）在
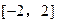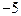
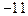
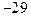
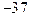
上有最大值3，那么此函数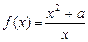在
在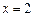
处取极值，则
.
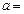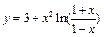
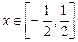的最大值与最小值分别为M,m，则M+m =