题目内容
设函数f(x)在区间[a,b]上满足f′(x)<0,则f(x)在[a,b]上的最小值为______,最大值为____________.
f(b) f(a)
本题考查在闭区间上可导函数的单调性、极值、最值与导数符号的关系.
因为函数f(x)在[a,b]上可导,并且f′(x)<0,所以函数f(x)在[a,b]上为单调递减函数,最小值为f(b),最大值为f(a).
因为函数f(x)在[a,b]上可导,并且f′(x)<0,所以函数f(x)在[a,b]上为单调递减函数,最小值为f(b),最大值为f(a).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
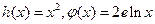 (其中e为自然对数)
(其中e为自然对数)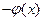 的极值。
的极值。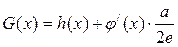 (常数a>0),当x>1时,求函数G(x)的单调区
(常数a>0),当x>1时,求函数G(x)的单调区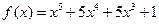 在区间
在区间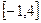 上的最大值与最小值。
上的最大值与最小值。 ,函数
,函数 的最大值为
的最大值为 ,最小值为
,最小值为 ,求
,求 的值。
的值。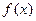 的定义域为开区间
的定义域为开区间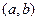 ,导函数
,导函数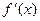 在
在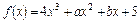 的图象在
的图象在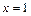 处的切线方程为
处的切线方程为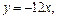
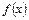 的解析式;
的解析式;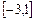 上的最值。
上的最值。