题目内容
.函数f(x)=x3＋x2－x在区间［－2，1］上的最大值和最小值分别是
A．1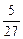，－ | B．1，－2 |
| C．2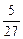，－ | D．2，－2 |
B
本题考查闭区间上连续函数的最值求解的基本方法.它的求解过程可分两步:第一步，求(a,b)内的极值；第二步，比较各极值与端点值的大小，求得最值.
∵f(x)=x3＋x2－x,∴f′(x)=3x2＋2x－1.
令3x2＋2x－1=0,得x1=－1,x2=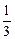
.
∵f(－2)=(－2)3＋(－2)2－(－2)=－2,f(－1)=1,f(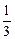)=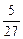－,f(1)=1,
∴f(x)max=1,f(x)min=－2.
∵f(x)=x3＋x2－x,∴f′(x)=3x2＋2x－1.
令3x2＋2x－1=0,得x1=－1,x2=
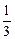.∵f(－2)=(－2)3＋(－2)2－(－2)=－2,f(－1)=1,f(
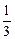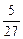)=－,f(1)=1,∴f(x)max=1,f(x)min=－2.
练习册系列答案
名校课堂系列答案
相关题目
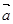=(1,1)，设f(x)=
·
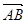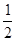x
≤f(x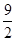
m-3都恒成立，求实数m的取值范围.
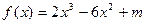（m为常数）在
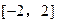上有最大值3，那么此函数在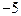
（
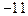
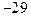
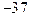
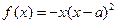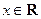），其中
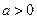，求函数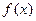
的极大值和极小值．
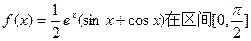上的值域是 。
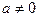，函数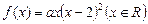
．
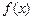有极大值32，求实数
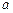的值；(Ⅱ)若对
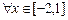，不等式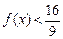
恒成立，求实数
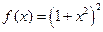的极值情况是： 极大值； 极小值（填“存在”或“不存在”）。