题目内容
在数列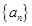 中,
中,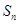 是数列
是数列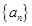 前
前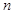 项和,
项和,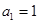 ,当
,当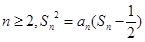
(1)证明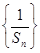 为等差数列;;
为等差数列;;
(2)设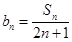 求数列
求数列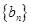 的前
的前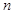 项和
项和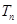 ;
;
(3)是否存在自然数m,使得对任意自然数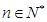 ,都有
,都有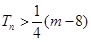 成立?若存在,
成立?若存在,
求出m 的最大值;若不存在,请说明理由。
(1)利用等差数列定义证明即可;(2 )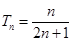 ;(3)m=9
;(3)m=9
解析试题分析:(1)
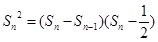 ,
, ,
,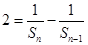 ,
,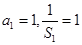 数列
数列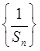 是以1为首项,2为公差的等差数列,
是以1为首项,2为公差的等差数列, ,
, ,
,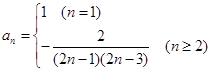
(2 ) 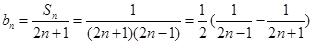
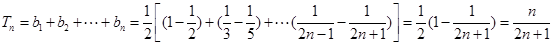
(3)令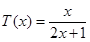 则
则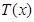 在
在 上是增函数,当
上是增函数,当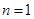 时,
时,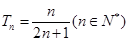 取得最小值
取得最小值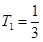 ,依题意可知,要使得对任意
,依题意可知,要使得对任意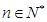 ,都有
,都有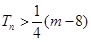 ,只要
,只要 ,
, ,
,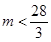 ,
,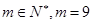
考点:本题考查了数列的通项及求和
点评:数列的通项公式及前n项和是数列的重点内容,数列的大题对逻辑推理能力有较高的要求,在数列中突出考查学生的理性思维,重点关注等差、等比数列的通项公式,错位相减法、裂项相消法等求数列的前n项的和等等

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
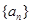 满足
满足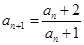 ,且
,且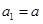 ,
,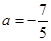 时,求出数列
时,求出数列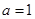 时,设
时,设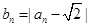 ,证明:
,证明: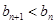 ;
;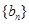 的前
的前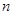 项和为
项和为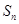 ,证明:
,证明: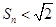 .
.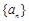 是等比数列,
是等比数列,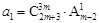 ,公比
,公比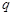 是
是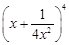 的展开式中的第二项(按x的降幂排列).
的展开式中的第二项(按x的降幂排列).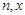 表示通项
表示通项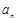 与前n项和
与前n项和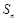 ;
;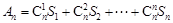 ,用
,用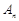 .
.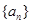 的前
的前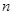 项和
项和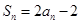 .数列
.数列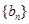 满足:
满足: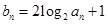 .
.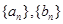 的通项
的通项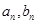 .并比较
.并比较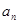 与
与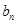 的大小;
的大小;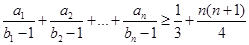 .
.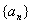 是各项都为正数的等比数列,
是各项都为正数的等比数列, 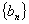 是等差数列,且
是等差数列,且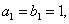 ,
,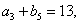
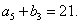
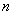 项和为
项和为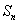 ,求证:
,求证: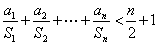 ;
;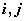 均为正整数,且
均为正整数,且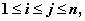 记所有可能乘积
记所有可能乘积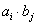 的和
的和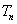 ,求证:
,求证: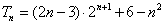 .
.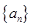 的前
的前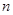 项和
项和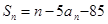 ,
,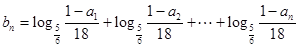 ,求数列
,求数列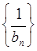 的前
的前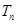 .
.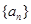 的前
的前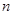 项和为
项和为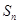 ,
,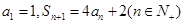 .
.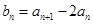 ,求
,求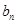 ;
;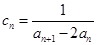 ,求
,求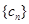 的前6项和
的前6项和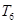 .
.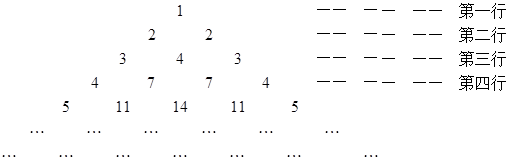
 行的第二个数为
行的第二个数为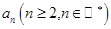
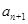 与
与 的递推关系(不必证明),并求出
的递推关系(不必证明),并求出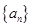 的通项公式
的通项公式 的通项公式为
的通项公式为
 的值;
的值; 的值,并用数学归纳法证明你的猜想.
的值,并用数学归纳法证明你的猜想.