题目内容
已知数列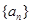 满足
满足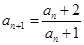 ,且
,且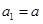 ,
,
(1)当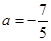 时,求出数列
时,求出数列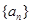 的所有项;
的所有项;
(2)当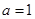 时,设
时,设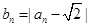 ,证明:
,证明: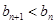 ;
;
(3)设(2)中的数列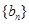 的前
的前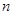 项和为
项和为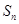 ,证明:
,证明: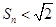 .
.
(1)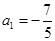 ,
,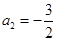 ,
,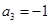 ;(2)详见解析;(3)详见解析.
;(2)详见解析;(3)详见解析.
解析试题分析:(1)先将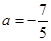 代入找出递推公式,逐一求出数列的每一项;(2)通过式子的变形找出
代入找出递推公式,逐一求出数列的每一项;(2)通过式子的变形找出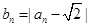 的形式,利用放缩法比较大小;(3)放缩法求出解析式,再利用等比数列得求和公式求和.
的形式,利用放缩法比较大小;(3)放缩法求出解析式,再利用等比数列得求和公式求和.
试题解析: (1)证明:∵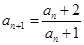 ,
,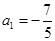 ,
,
∴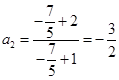 ,
, ,
,
由于当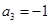 时,使递推式右边的分母为零。
时,使递推式右边的分母为零。
∴数列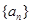 只有三项:
只有三项: . (3分)
. (3分)
(2)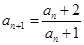 ,
,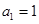 易知:
易知: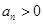 ,
,
又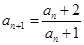
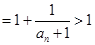 ,
,
∴ (5分)
(5分)
由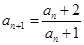
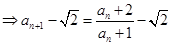
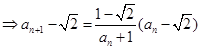
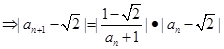
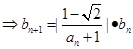 ,
,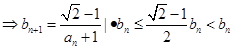
即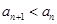 (8分)
(8分)
(3)由(2)知:  ,
,
∴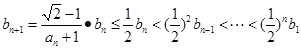
∵ ,
,
∴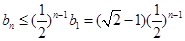 (11分)
(11分)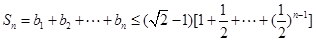
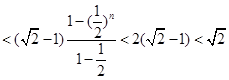 ,
,
∴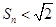 (13分)
(13分)
考点:1.由递推公式求数列的每一项;2.放缩法比较大小;3.等比数列求和.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
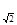 an}的前n项和为Tn.求使Tn>bn的最小正整数n.
an}的前n项和为Tn.求使Tn>bn的最小正整数n.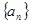 的前n项和为
的前n项和为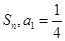 且
且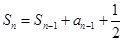 ,数列
,数列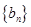 满足
满足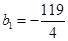 且
且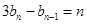
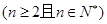 .
.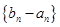 为等比数列;
为等比数列;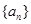 满足:
满足: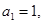
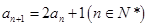

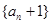 为等比数列,并求出数列
为等比数列,并求出数列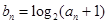 ,求数列
,求数列 的前
的前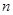 项和
项和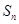 .
.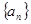 的前
的前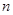 项和为
项和为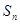 ,且
,且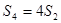 ,
,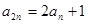 .
. 满足
满足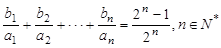 ,求
,求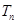 .
.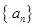 的任意连续三项均能构成一个三角形的三边长,则称
的任意连续三项均能构成一个三角形的三边长,则称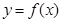 使得
使得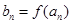 仍为一个“三角形”数列,则称
仍为一个“三角形”数列,则称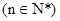 .
.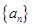 是首项为2,公差为1的等差数列,若
是首项为2,公差为1的等差数列,若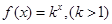 是数列
是数列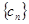 的首项为2010,
的首项为2010, 是数列
是数列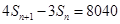 ,证明
,证明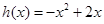 ,
,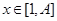 ,和数列1,
,和数列1,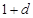 ,
,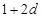 ,(
,(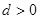 )提出一个正确的命题,并说明理由.
)提出一个正确的命题,并说明理由.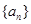 中,
中,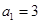 ,前
,前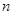 项和为
项和为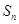 ,等比数列
,等比数列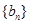 各项均为正数,
各项均为正数,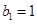 ,且
,且 ,
,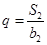 .
.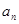 与
与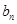 ;(2)求
;(2)求 .
.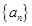 中,
中,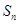 是数列
是数列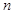 项和,
项和,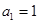 ,当
,当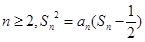
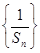 为等差数列;;
为等差数列;;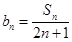 求数列
求数列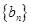 的前
的前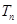 ;
;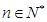 ,都有
,都有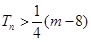 成立?若存在,
成立?若存在, 的前n项和为
的前n项和为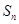 .已知
.已知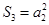 ,且
,且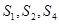 成等比数列,求
成等比数列,求