题目内容
5.已知函数f(x)=|log2(x-1)|,g(x)=($\frac{1}{2}$)x,则图象交于A(x1,y1),B(x2,y2)两点,则( )| A. | x1•x2<1 | B. | x1+x2>5 | C. | x1+x2>x1•x2 | D. | x1+x2<x1•x2 |
分析 作出两个函数的图象,不妨设x1<x2,利用对数的运算性质和指数函数的运算性质进行判断即可.
解答  解:不妨设x1<x2,
解:不妨设x1<x2,
作出f(x)和g(x)的图象,由图象知x1<2,x2>2,
则f(x1)=|log2(x1-1)|=-log2(x1-1),f(x2)=|log2(x2-1)|=log2(x2-1),
则f(x2)-f(x1)=log2(x2-1)+log2(x1-1)=log2(x1-1)(x2-1)=$(\frac{1}{2})^{{x}_{2}}$-$(\frac{1}{2})^{{x}_{1}}$<0,
即(x1-1)(x2-1)<1,
即x1x2-(x1+x2)+1<1,
即x1+x2>x1•x2,
故选:C
点评 本题主要考查对数函数和指数函数的应用,利用数形结合是解决本题的关键.综合性较强,有一定的难度.

练习册系列答案
相关题目
13.函数y=ecosx(-π≤x≤π)的大致图象为( )
| A. | 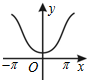 | B. | 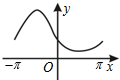 | C. | 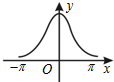 | D. |  |
14.定义集合A与B的运算:A⊙B={x|x∈A或x∈B,且x∉A∩B},已知集合A={1,2,3,4},B={3,4,5,6,7},则(A⊙B)⊙B为( )
| A. | {1,2,3,4,5,6,7} | B. | {1,2,3,4} | C. | {1,2} | D. | {3,4,5,6,7} |