题目内容
13.函数y=ecosx(-π≤x≤π)的大致图象为( )| A. | 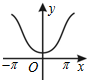 | B. | 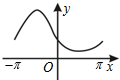 | C. | 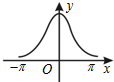 | D. |  |
分析 根据复合函数的单调性,同增异减,即可判断.
解答 解:设u=cosx,则u=cosx在[-π,0)为减函数,在(0,π]上增函数,
因为y=eu在R上为增函数,
∴y=ecosx(-π≤x≤π)[-π,0)为减函数,在(0,π]上增函数,
故选:C.
点评 本题考查了复合函数的单调性质,属于基础题.

练习册系列答案
相关题目
1.设集合A={x|x2>4},B={x|x2+2x-3<0},则A∩B=( )
| A. | R | B. | (2,3) | C. | (-3,-2) | D. | (-3,-2)∪(2,+∞) |
8.某流程图如图所示,现输入如下四个函数,则可以输出的函数是( )


| A. | f(x)=$\frac{|x|}{x}$ | B. | f(x)=$\frac{cosx}{x}$(-$\frac{π}{2}$<x<$\frac{π}{2}$) | ||
| C. | f(x)=$\frac{{2}^{x}-1}{{2}^{x}+1}$ | D. | f(x)=x2ln(x2+1) |
18.设集合A={x|x|x2-x-2≥0},B={x|x>a},若A∩B={x|x≥2},则所有实数a组成的集合为( )
| A. | {a|a≥2} | B. | {a|a≤2} | C. | {a|-1≤a≤2} | D. | {a|-1≤a<2} |
5.已知函数f(x)=|log2(x-1)|,g(x)=($\frac{1}{2}$)x,则图象交于A(x1,y1),B(x2,y2)两点,则( )
| A. | x1•x2<1 | B. | x1+x2>5 | C. | x1+x2>x1•x2 | D. | x1+x2<x1•x2 |