题目内容
过双曲线C:
-
=1的右顶点做x轴的垂线,与C的一条渐近线相交于点A,若以C的右焦点为圆心、半径为4的圆经过A,O两点(O为坐标原点),则双曲线C的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:由题意,c=4,双曲线的一条渐近线方程为y=
x,求出A的坐标,利用右焦点F(4,0),|FA|=4,可求a,b,即可得出双曲线的方程.
| b |
| a |
解答:解:由题意,c=4,双曲线的一条渐近线方程为y=
x,
令x=a,则y=b,即A(a,b),
∵右焦点F(4,0),|FA|=4,
∴(a-4)2+b2=16,
∵a2+b2=16,
∴a=2,b=2
,
∴双曲线C的方程为
-
=1.
故选:A.
| b |
| a |
令x=a,则y=b,即A(a,b),
∵右焦点F(4,0),|FA|=4,
∴(a-4)2+b2=16,
∵a2+b2=16,
∴a=2,b=2
| 3 |
∴双曲线C的方程为
| x2 |
| 4 |
| y2 |
| 12 |
故选:A.
点评:本题考查双曲线的方程与性质,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
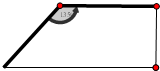 两直立矮墙成135°二面角,现利用这两面矮墙和篱笆围成一个面积为54m2的直角梯形菜园(墙足够长),则所用篱笆总长度的最小值为( )
两直立矮墙成135°二面角,现利用这两面矮墙和篱笆围成一个面积为54m2的直角梯形菜园(墙足够长),则所用篱笆总长度的最小值为( )| A、16m | ||
| B、18m | ||
| C、22.5m | ||
D、15
|
若p:φ=
+kπ,k∈Z,q:f(x)=sin(ωx+φ)(ω≠0)是偶函数,则p是q的( )
| π |
| 2 |
| A、充要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |
已知椭圆C:
+
=1(a>b>0)的左、右焦点为F1、F2,离心率为
,过F2的直线l交C于A、B两点,若△AF1B的周长为4
,则C的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知曲线C1:
+y2=1和C2:x2-y2=1的焦点分别为F1、F2,点M是C1和C2的一个交点,则△MF1F2的形状是( )
| x2 |
| 3 |
| A、锐角三角形 | B、直角三角形 |
| C、钝角三角形 | D、不能确定 |
已知M是x2=8y的对称轴与准线的交点,点N是其焦点,点P在该抛物线上,且满足|PM|=m|PN|,当m取得最大值时,点P恰在以M、N为焦点的双曲线上,则该双曲线的实轴长为( )
A、2(
| ||
B、4(
| ||
C、2(
| ||
D、4(
|
已知两点A(1,-2),B(-4,-2),以下列四条曲线:
①4x+2y=3;
②x2+y2=3;
③x2+2y2=3;
④x2-2y2=3.
其中存在点P,使|PA|=|PB|的曲线有( )
①4x+2y=3;
②x2+y2=3;
③x2+2y2=3;
④x2-2y2=3.
其中存在点P,使|PA|=|PB|的曲线有( )
| A、①③ | B、②④ | C、①②③ | D、②③④ |
已知函数f(x)=ex-ax-b,若f(x)≥0恒成立,则ab的最大值为( )
A、
| ||
| B、e2 | ||
| C、e | ||
D、
|
已知A(-4,2,3)关于xOz平面的对称点为A1,A1关于z轴的对称点为A2,则|AA2|等于( )
| A、8 | B、12 | C、16 | D、19 |