题目内容
5．已知a＞b＞0，且a+b=2，则$\frac{2}{a+3b}+\frac{1}{a-b}$的最小值为$\frac{3+2\sqrt{2}}{4}$．分析 利用“乘1法”与基本不等式的性质即可得出．
解答 解：∵（a+3b）+（a-b）=2（a+b）=4，
∴$\frac{1}{4}$[（a+3b）+（a-b）]=1，
∴$\frac{2}{a+3b}+\frac{1}{a-b}$
=$\frac{1}{4}$（$\frac{2}{a+3b}+\frac{1}{a-b}$）[（a+3b）+（a-b）]
=$\frac{1}{4}$[2+$\frac{2（a-b）}{a+3b}$+$\frac{a+3b}{a-b}$+1]
≥$\frac{1}{4}$[3+2$\sqrt{\frac{2（a-b）（a+3b）}{（a+3b）（a-b）}}$]
=$\frac{3+2\sqrt{2}}{4}$，
故答案为：$\frac{3+2\sqrt{2}}{4}$．
点评 本题考查了“乘1法”与基本不等式的性质，考查了变形能力，属于中档题．
练习册系列答案
相关题目
15．若x≥1，a=（$\frac{1}{3}$）${\;}^{{x}^{2}+1}$，b=（$\frac{1}{3}$）x+1，c=（$\frac{1}{3}$）2x，则下列关系中正确的是（ ）
| A． | lga≥lgb≥1gc | B． | lgb≥lgc≥lga | C． | lgb≥lga≥lgc | D． | 1gc≥1ga≥lgb |
20．
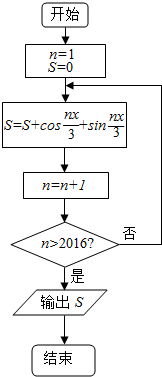如图所示程序框图中，输出S=（ ）
如图所示程序框图中，输出S=（ ）| A． | -1 | B． | 0 | C． | 1 | D． | $\sqrt{3}$ |
定义运算?，a?b=S的运算原理如伪代码所示，则式子5?3+2?4=32．
15．设复数z=（x-1）+yi（x∈R，y≥0），若|z|≤1，则y≥x的概率为（ ）
| A． | $\frac{3}{4}+\frac{1}{2π}$ | B． | $\frac{1}{4}-\frac{1}{2π}$ | C． | $\frac{1}{2}-\frac{1}{π}$ | D． | $\frac{1}{2}+\frac{1}{π}$ |