题目内容
(12分) 若二次函数f(x)=ax2+bx+c(a≠0)的图象关于y轴对称,
且f(-2)>f(3),设m>-n>0.
(1) 试证明函数f(x)在(0,+∞)上是减函数;
(2) 试比较f(m)和f(n)的大小,并说明理由.
且f(-2)>f(3),设m>-n>0.
(1) 试证明函数f(x)在(0,+∞)上是减函数;
(2) 试比较f(m)和f(n)的大小,并说明理由.
(1)见解析;(2)f(m)<f(n).
(1)∵f(x)=ax2+bx+c(a≠0)的图象关于y轴对称,
∴对任意x∈R,恒有f(-x)=f(x),即a(-x)2+b(-x)+c=ax2+bx+c恒成立,
据此可求出b="0." f(x)=ax2+c.再根据f(-2)>f(3),且f(-2)=f(2),
得f(2)>f(3),因而a<0.且f(x)在(0,+∞)上是减函数..
(2)∵m>-n>0,∴f(m)<f(-n).,再根据f(-n)=f(n),可得f(m)<f(n)..
∵f(x)=ax2+bx+c(a≠0)的图象关于y轴对称,
∴对任意x∈R,恒有f(-x)=f(x),
即a(-x)2+b(-x)+c=ax2+bx+c恒成立.
∴2bx=0对任意x∈R恒成立.
∴b=0.
∴f(x)=ax2+c.
∵f(-2)>f(3),且f(-2)=f(2),
∴f(2)>f(3).
∴a<0.且f(x)在(0,+∞)上是减函数.
又∵m>-n>0,
∴f(m)<f(-n).
而f(-n)=f(n),
∴f(m)<f(n).
∴对任意x∈R,恒有f(-x)=f(x),即a(-x)2+b(-x)+c=ax2+bx+c恒成立,
据此可求出b="0." f(x)=ax2+c.再根据f(-2)>f(3),且f(-2)=f(2),
得f(2)>f(3),因而a<0.且f(x)在(0,+∞)上是减函数..
(2)∵m>-n>0,∴f(m)<f(-n).,再根据f(-n)=f(n),可得f(m)<f(n)..
∵f(x)=ax2+bx+c(a≠0)的图象关于y轴对称,
∴对任意x∈R,恒有f(-x)=f(x),
即a(-x)2+b(-x)+c=ax2+bx+c恒成立.
∴2bx=0对任意x∈R恒成立.
∴b=0.
∴f(x)=ax2+c.
∵f(-2)>f(3),且f(-2)=f(2),
∴f(2)>f(3).
∴a<0.且f(x)在(0,+∞)上是减函数.
又∵m>-n>0,
∴f(m)<f(-n).
而f(-n)=f(n),
∴f(m)<f(n).

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
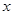 (万元)时,产品的销售量将是原销售量的
(万元)时,产品的销售量将是原销售量的 倍,且
倍,且 成本费
成本费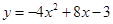

 ,则
,则 的最小值等于 .
的最小值等于 .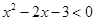 的解集为
的解集为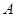 ,不等式
,不等式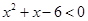 的解集为
的解集为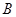 。
。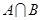 ;
; 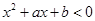 的解集为
的解集为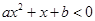 的解集。
的解集。 对任意实数
对任意实数 都有
都有 ,那么( )
,那么( )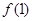 <
< <
<
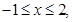 则
则 的最大值与最小值之差为 .
的最大值与最小值之差为 .  的值域为 。
的值域为 。 
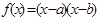 (其中
(其中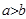 )的图象如图1所示,则函数
)的图象如图1所示,则函数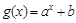 的图象是图2中的:
的图象是图2中的: