题目内容
设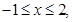
则
的最大值与最小值之差为 .
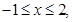则的最大值与最小值之差为 . 1
：∵-1≤x≤2，∴x-2≤0，x+2＞0，∴当2≥x＞0时，|x-2|-
|x|+|x+2|=2-x-x+x+2=4-x；
当-1≤x＜0时，|x-2|-|x|+|x+2|=2-x+x+x+2=4+x，当x=0时，取得最大值为4，x=2时取得最小值，最小值为3，则最大值与最小值之差为1．故答案为：1
|x|+|x+2|=2-x-x+x+2=4-x；当-1≤x＜0时，|x-2|-
|x|+|x+2|=2-x+x+x+2=4+x，当x=0时，取得最大值为4，x=2时取得最小值，最小值为3，则最大值与最小值之差为1．故答案为：1
练习册系列答案
全能练考卷系列答案
相关题目
，若
的解集为
，函数
，（1）求
与
的值；（2）
是二次函数，且满足
，
在
单调，求
的取值范围。
，则
的解集为 ( )
, 
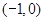
，则函数值
的取值范围是（ ）
≤
}
，
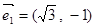，若
，
，若
，则实数
和
满足的一个关系式是 ，
的最小值为 ．
，若
在区间
上的最大值为1，则
的取