题目内容
设向量a=(x+1,y),b=(x-1,y),点P(x,y)为动点,已知|a|+|b|=4.
(Ⅰ)求点P的轨迹方程;
(Ⅱ)设点P的轨迹与x轴负半轴交于点A,过点F(1,0)的直线交点P的轨迹于B、C两点,试推断△ABC的面积是否存在最大值?若存在,求其最大值;若不存在,请说明理由.
(Ⅰ)求点P的轨迹方程;
(Ⅱ)设点P的轨迹与x轴负半轴交于点A,过点F(1,0)的直线交点P的轨迹于B、C两点,试推断△ABC的面积是否存在最大值?若存在,求其最大值;若不存在,请说明理由.
(Ⅰ)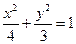 (Ⅱ)△ABC的面积存在最大值,其最大值为
(Ⅱ)△ABC的面积存在最大值,其最大值为
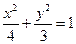 (Ⅱ)△ABC的面积存在最大值,其最大值为
(Ⅱ)△ABC的面积存在最大值,其最大值为
(Ⅰ)由已知,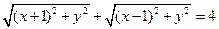 (1分)
(1分)
所以动点P的轨迹M是以点 为焦点,长轴长为4的椭圆. (3分)
为焦点,长轴长为4的椭圆. (3分)
因为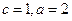 ,则
,则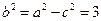 . (4分)
. (4分)
故动点P的轨迹M的方程是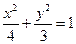 . (5分)
. (5分)
(Ⅱ)设直线BC的方程为 ,
,
由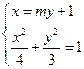
 . (6分)
. (6分)
设点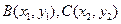 ,则
,则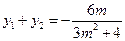 ,
,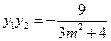 . (7分)
. (7分)
所以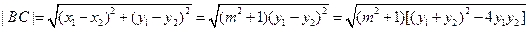
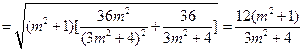 . (8分)
. (8分)
由题设,点A的坐标是(-2,0),则点A到直线BC的距离 . (9分)
. (9分)
所以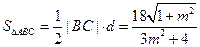 .
.
令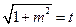 ,则
,则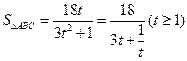 . (10分)
. (10分)
设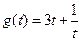 ,则
,则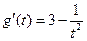 .因为当
.因为当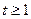 时,
时,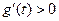 ,则函数
,则函数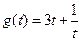 在
在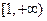 上是增函数. (11分)
上是增函数. (11分)
所以当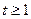 时,
时,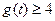 ,从而
,从而 ,所以
,所以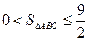 . (12分)
. (12分)
故△ABC的面积存在最大值,其最大值为 . (13分)
. (13分)
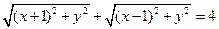 (1分)
(1分)所以动点P的轨迹M是以点
 为焦点,长轴长为4的椭圆. (3分)
为焦点,长轴长为4的椭圆. (3分)因为
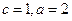 ,则
,则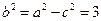 . (4分)
. (4分)故动点P的轨迹M的方程是
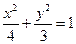 . (5分)
. (5分)(Ⅱ)设直线BC的方程为
 ,
,由
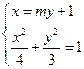
 . (6分)
. (6分)设点
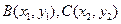 ,则
,则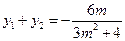 ,
,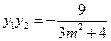 . (7分)
. (7分)所以
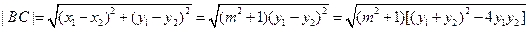
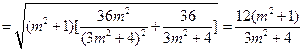 . (8分)
. (8分)由题设,点A的坐标是(-2,0),则点A到直线BC的距离
 . (9分)
. (9分)所以
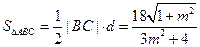 .
.令
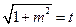 ,则
,则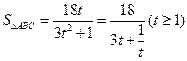 . (10分)
. (10分)设
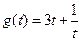 ,则
,则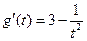 .因为当
.因为当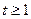 时,
时,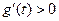 ,则函数
,则函数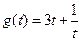 在
在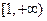 上是增函数. (11分)
上是增函数. (11分)所以当
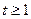 时,
时,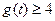 ,从而
,从而 ,所以
,所以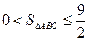 . (12分)
. (12分)故△ABC的面积存在最大值,其最大值为
 . (13分)
. (13分)
练习册系列答案
相关题目
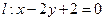 过椭圆的左焦点
过椭圆的左焦点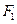 和一个顶点
和一个顶点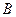 ,该椭圆的离心率为
,该椭圆的离心率为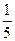
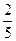
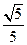
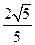
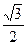 ,与直线x+y-1=0相交于两点M、N,且以
,与直线x+y-1=0相交于两点M、N,且以 为直径的圆经过坐标原点.求椭圆的方程.
为直径的圆经过坐标原点.求椭圆的方程.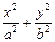 =1(a>b>0)的左、右两个焦点.
=1(a>b>0)的左、右两个焦点.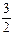 )到F1、F2两点的距离之和等于4,写出椭圆C的方程和焦点坐标;
)到F1、F2两点的距离之和等于4,写出椭圆C的方程和焦点坐标;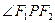 最大,说明理由,并求出最大值。
最大,说明理由,并求出最大值。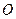 为中心的椭圆的一条准线方程为
为中心的椭圆的一条准线方程为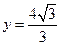 ,离心率
,离心率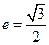 ,
,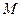 是椭圆上的动点。
是椭圆上的动点。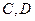 的坐标分别是
的坐标分别是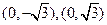 ,求
,求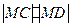 的最大值;
的最大值;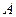 的坐标为
的坐标为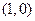 ,
,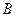 是圆
是圆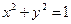 上的点,
上的点,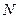 是点
是点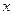 轴上的射影,点
轴上的射影,点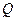 满足条件:
满足条件: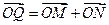 ,
,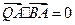 ,求线段
,求线段 的中点
的中点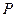 的轨迹方程。
的轨迹方程。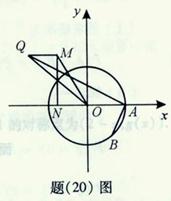
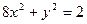 上两点,O是坐标原点,定点
上两点,O是坐标原点,定点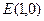 ,向量
,向量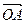 .
.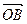 在向量
在向量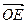 方向上的投影分别是m.n ,且
方向上的投影分别是m.n ,且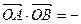 7mn ,动点P满足
7mn ,动点P满足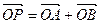
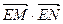 的取值范围。
的取值范围。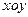 中,向量
中,向量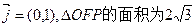 ,且
,且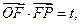
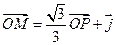 .(1)设
.(1)设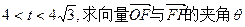 的取值范围;
的取值范围;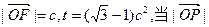 取最小值时,求椭圆的方程.
取最小值时,求椭圆的方程.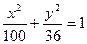 上的点P到它的左准线的距离是10,那么点P 到它的右焦点的距离是( )
上的点P到它的左准线的距离是10,那么点P 到它的右焦点的距离是( )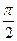 ),方程
),方程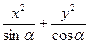 =1表示焦点在x轴上的椭圆,则α的取值范围是( )
=1表示焦点在x轴上的椭圆,则α的取值范围是( )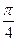 )
)