题目内容
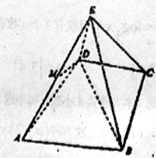
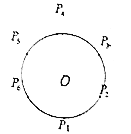
【题目】如图,设![]() 为单位圆上逆时针均匀分布的六个点,现从这六个点中任选其中三个不同点构成一个三角形,记该三角形的面积为随机变量
为单位圆上逆时针均匀分布的六个点,现从这六个点中任选其中三个不同点构成一个三角形,记该三角形的面积为随机变量![]() .
.
(1)求![]() 的概率;
的概率;
(2)求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】试题分析:(1)由排列组合可求得从六外点任选三个不同点构成一个三角形的所有选法,其中面积为![]() 的是一个角为
的是一个角为![]() 的直角三角形,由古典概型可求得概率;(2)先写出
的直角三角形,由古典概型可求得概率;(2)先写出![]() 的所有可能取值,再求出所对应的概率,可写出
的所有可能取值,再求出所对应的概率,可写出![]() 的分布列,进一步求出数学期望.
的分布列,进一步求出数学期望.
试题解析:(1)从六个点任选三个不同点构成一个三角形共有![]() 种不同选法,
种不同选法,
其中![]() 的为有一个是
的为有一个是![]() 的直角三角形(如:
的直角三角形(如: ![]() )共
)共![]() 种,
种,
所以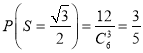 .
.
(2)![]() 的所有可能取值为
的所有可能取值为![]() ,
,
![]() 的为顶角是
的为顶角是![]() 的等腰三角形(如
的等腰三角形(如![]() ),共
),共![]() 种,所以
种,所以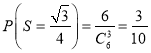 ,
,
![]() 的为等边三角形(如:
的为等边三角形(如: ![]() )共
)共![]() 种,所以
种,所以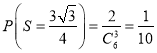 ,
,
又由(1)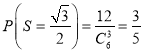 ,故
,故![]() 的分布列为:
的分布列为:
|
|
|
|
|
|
|
|
所以![]() .
.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
【题目】某商店为了吸引顾客,设计了一个摸球小游戏,顾客从装有1个红球,1个白球,3个黑球的袋中一次随机的摸2个球,设计奖励方式如下表:
结果 | 奖励 |
1红1白 | 10元 |
1红1黑 | 5元 |
2黑 | 2元 |
1白1黑 | 不获奖 |
(1)某顾客在一次摸球中获得奖励X元,求X的概率分布表与数学期望;
(2)某顾客参与两次摸球,求他能中奖的概率.