Question

【题目】如图，在矩形ABCD中，已知AB＝a，BC＝b(a>b)，在AB，AD，CB，CD上，分别截取AE＝AH＝CF＝CG＝x(x>0)，设四边形EFGH的面积为y.

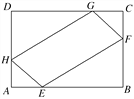
(1)写出四边形EFGH的面积y与x之间的函数关系；

(2)求当x为何值时y取得最大值，最大值是多少？

Answer 1

【答案】（1）y＝－2x2＋(a＋b)x(0<x≤b)；（2）当x＝b时，ymax＝(a－b)b,当时，ymax＝.

【解析】试题分析：（1）由关系S四边形EFGH=S矩形ABCD-S△AEH-S△CEF-S△BEF-S△DGH，即可求出表达式；
（2）利用（1）求出的关系式，再利用二次函数的性质即可求出最大值．

试题解析：

(1)∵△AEH≌△CFG，△EBF≌△GDH，

∴

．

(2)y＝－2.

①如图1，当b≥，即a>b≥时，

当x＝时，ymax＝；

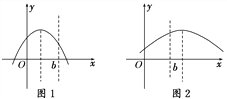
②如图2，当0<b<，即0<b<时，

y在区间(0，b]上是增函数，

当x＝b时，ymax＝(a－b)b.