Question

【题目】(本小题满分12分) 函数f(x)是定义在R上的偶函数,已知当x≤0时,f(x)=x2+4x+3.

（1）求函数f(x)的解析式;

（2）画出函数的图象，并写出函数f(x)的单调区间;

（3）求f(x)在区间[-1,2]上的值

Answer 1

【答案】(1) (2)详见解析（3）

【解析】试题分析：（1）设，则，利用当时， ，结合函数为偶函数，即可求得函数解析式；（2）根据图象，可得函数的单调递增区间；（3）确定函数在区间上的单调性，求出函数 的最值，从而可得函数在区间上的值域.

试题解析：(1)因为函数f(x)是定义在R上的偶函数,所以对任意的x∈R都有f(-x)=f(x)成立,

所以当x>0时,-x<0,即f(x)=f(-x)=(-x)2+4(-x)+3=x2-4x+3,

所以f(x)=

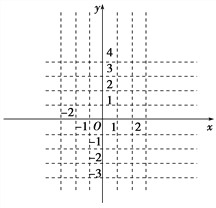
（2）

函数图象如图，由图知函数f(x)的单调递增区间为[-2,0]和[2,+∞). 单调递减区间为（-∞, -2]和[0，2] .

（3）由②知函数f(x)在[-1,0]上单调递增,所以f(-1)≤f(x)≤f(0),

即0≤f(x)≤3;在区间[0,2]上单调递减,

所以f(2)≤f(x)≤f(0),即-1≤f(x)≤3,

所以函数f(x)在区间[-1,2]上的值域为[-1,3].

【方法点晴】本题主要考查函数的奇偶性、函数的解析式、函数的单调性，属于中档题.函数单调性的应用比较广泛，是每年高考的重点和热点内容．归纳起来，常见的命题探究角度有：（1）求函数的值域或最值；（2）比较两个函数值或两个自变量的大小；（3）解函数不等式；（4）求参数的取值范围或值．