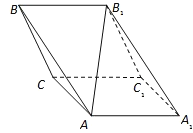
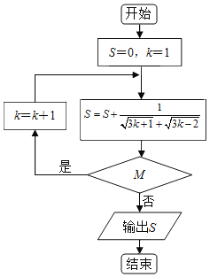
ЬтФПФкШн
ЁОЬтФПЁПЩшМЏКЯ![]() ЁЂ
ЁЂ![]() ОљЮЊЪЕЪ§МЏ
ОљЮЊЪЕЪ§МЏ![]() ЕФзгМЏЃЌМЧЃК
ЕФзгМЏЃЌМЧЃК![]() ЃЛ
ЃЛ
ЃЈ1ЃЉвбжЊ![]() ЃЌ
ЃЌ![]() ЃЌЪдгУСаОйЗЈБэЪО
ЃЌЪдгУСаОйЗЈБэЪО![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЩш![]() ЃЌЕБ
ЃЌЕБ![]() ЃЌЧв
ЃЌЧв![]() ЪБЃЌЧњЯп
ЪБЃЌЧњЯп![]() ЕФНЙОрЮЊ
ЕФНЙОрЮЊ![]() ЃЌШчЙћ
ЃЌШчЙћ![]() ЃЌ
ЃЌ![]() ЃЌЩш
ЃЌЩш![]() жаЕФЫљгадЊЫижЎКЭЮЊ
жаЕФЫљгадЊЫижЎКЭЮЊ![]() ЃЌЖдгкТњзу
ЃЌЖдгкТњзу![]() ЃЌЧв
ЃЌЧв![]() ЕФШЮвте§ећЪ§
ЕФШЮвте§ећЪ§![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЃЌВЛЕШЪН
ЃЌВЛЕШЪН![]() КуГЩСЂЃЌЧѓЪЕЪ§
КуГЩСЂЃЌЧѓЪЕЪ§![]() ЕФзюДѓжЕЃЛ
ЕФзюДѓжЕЃЛ
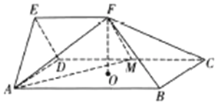
ЃЈ3ЃЉШєећЪ§МЏКЯ![]() ЃЌдђГЦ
ЃЌдђГЦ![]() ЮЊЁАздЩњМЏЁБЃЌШєШЮвтвЛИіе§ећЪ§ОљЮЊећЪ§МЏКЯ
ЮЊЁАздЩњМЏЁБЃЌШєШЮвтвЛИіе§ећЪ§ОљЮЊећЪ§МЏКЯ![]() ЕФФГИіЗЧПегаЯозгМЏжаЫљгадЊЫиЕФКЭЃЌдђГЦ
ЕФФГИіЗЧПегаЯозгМЏжаЫљгадЊЫиЕФКЭЃЌдђГЦ![]() ЮЊЁА
ЮЊЁА![]() ЕФЛљЕзМЏЁБЃЌЮЪЃКЪЧЗёДцдквЛИіећЪ§МЏКЯМШЪЧздЩњМЏгжЪЧ
ЕФЛљЕзМЏЁБЃЌЮЪЃКЪЧЗёДцдквЛИіећЪ§МЏКЯМШЪЧздЩњМЏгжЪЧ![]() ЕФЛљЕзМЏЃПЧыЫЕУїРэгЩЃЎ
ЕФЛљЕзМЏЃПЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЈ2ЃЉ
ЃЈ2ЃЉ![]() ЃЈ3ЃЉДцдкЃЌРэгЩМћНтЮі
ЃЈ3ЃЉДцдкЃЌРэгЩМћНтЮі
ЁОНтЮіЁП
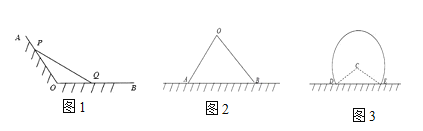
ЃЈ1ЃЉИљОнаТЖЈвх![]() ЃЌНсКЯвбжЊжаЕФМЏКЯ
ЃЌНсКЯвбжЊжаЕФМЏКЯ![]() ЁЂ
ЁЂ![]() ЃЌПЩЕУД№АИЃЛ
ЃЌПЩЕУД№АИЃЛ
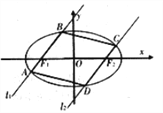
ЃЈ2ЃЉЧњЯп![]() БэЪОЫЋЧњЯпЃЌНјЖјПЩЕУ
БэЪОЫЋЧњЯпЃЌНјЖјПЩЕУ![]() ЃЌ
ЃЌ![]() ЃЌдђ
ЃЌдђ![]()
![]() ЃЌНсКЯ
ЃЌНсКЯ![]() Чв
Чв![]() МАЛљБОВЛЕШЪНЃЌПЩЕУ
МАЛљБОВЛЕШЪНЃЌПЩЕУ![]() НјЖјЕУЕНД№АИЃЛ
НјЖјЕУЕНД№АИЃЛ
ЃЈ3ЃЉЩшећЪ§МЏКЯ![]() ЃЌЦфжа
ЃЌЦфжа![]() ЮЊьГВЈФЧЦѕЪ§СаЃЌМД
ЮЊьГВЈФЧЦѕЪ§СаЃЌМД![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЂйгЩ![]() ЕУЃК
ЕУЃК![]() ЃЌПЩЕУ
ЃЌПЩЕУ![]() ЪЧздЩњМЏЃЛ
ЪЧздЩњМЏЃЛ
ЂкЖдгкШЮвт![]() ЃЌЖдгкШЮвЛе§ећЪ§
ЃЌЖдгкШЮвЛе§ећЪ§![]() ЃЌДцдкМЏКЯ
ЃЌДцдкМЏКЯ![]() ЕФвЛИігаЯозгМЏ
ЕФвЛИігаЯозгМЏ![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЃЌЃЈ
ЃЌЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌдйгУЪ§бЇЙщФЩЗЈжЄУїМЏКЯ
ЃЉЃЌдйгУЪ§бЇЙщФЩЗЈжЄУїМЏКЯ![]() гжЪЧ
гжЪЧ![]() ЕФЛљЕзМЏЃЎ
ЕФЛљЕзМЏЃЎ
НтЃКЃЈ1ЃЉЁп![]() ЃЛ
ЃЛ
ЕБ![]() ЃЌ
ЃЌ![]() ЪБЃЌ
ЪБЃЌ
![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЧњЯп![]() ЃЌМД
ЃЌМД![]() ЃЌдк
ЃЌдк![]() ЪББэЪОЫЋЧњЯпЃЌ
ЪББэЪОЫЋЧњЯпЃЌ
ЙЪ ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() жаЕФЫљгадЊЫижЎКЭЮЊ
жаЕФЫљгадЊЫижЎКЭЮЊ![]()
![]() ЃЌ
ЃЌ
Ёр![]()
![]() ЃЌ
ЃЌ
Ёп![]() ЃЌЧв
ЃЌЧв![]() ЃЌ
ЃЌ
Ёр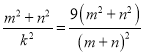
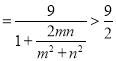 ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
МДЪЕЪ§![]() ЕФзюДѓжЕЮЊ
ЕФзюДѓжЕЮЊ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉДцдквЛИіећЪ§МЏКЯМШЪЧздЩњМЏгжЪЧ![]() ЕФЛљЕзМЏЃЌРэгЩШчЯТЃК
ЕФЛљЕзМЏЃЌРэгЩШчЯТЃК
ЩшећЪ§МЏКЯ![]() ЃЌЦфжа
ЃЌЦфжа![]() ЮЊьГВЈФЧЦѕЪ§СаЃЌ
ЮЊьГВЈФЧЦѕЪ§СаЃЌ
МД![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЯТжЄЃКећЪ§МЏКЯ![]() МШЪЧздЩњМЏгжЪЧ
МШЪЧздЩњМЏгжЪЧ![]() ЕФЛљЕзМЏЃЌ
ЕФЛљЕзМЏЃЌ
ЂйгЩ![]() ЕУЃК
ЕУЃК![]() ЃЌ
ЃЌ
ЙЪ![]() ЪЧздЩњМЏЃЛ
ЪЧздЩњМЏЃЛ
ЂкЖдгкШЮвт![]() ЃЌЖдгкШЮвЛе§ећЪ§
ЃЌЖдгкШЮвЛе§ећЪ§![]() ЃЌДцдкМЏКЯ
ЃЌДцдкМЏКЯ![]() ЕФвЛИігаЯозгМЏ
ЕФвЛИігаЯозгМЏ![]() ЃЌ
ЃЌ
ЪЙЕУ![]() ЃЌЃЈ
ЃЌЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЕБ![]() ЪБЃЌгЩ
ЪБЃЌгЩ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌжЊНсТлГЩСЂЃЛ
ЃЌжЊНсТлГЩСЂЃЛ
МйЩшНсТлЖд![]() ЪБГЩСЂЃЌ
ЪБГЩСЂЃЌ
дђ![]() ЪБЃЌжЛаыЖдШЮКЮећЪ§
ЪБЃЌжЛаыЖдШЮКЮећЪ§![]() ЬжТлЃЌ
ЬжТлЃЌ
Шє![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЙЪ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
гЩЙщФЩМйЩшЃЌ![]() ПЩвдБэЪОЮЊМЏКЯ
ПЩвдБэЪОЮЊМЏКЯ![]() жагаЯоИіОјЖджЕаЁгк
жагаЯоИіОјЖджЕаЁгк![]() ЕФдЊЫиЕФКЭЃЎ
ЕФдЊЫиЕФКЭЃЎ
вђЮЊ![]() ЃЌ
ЃЌ
Ыљвд![]() ПЩвдБэЪОЮЊМЏКЯ
ПЩвдБэЪОЮЊМЏКЯ![]() жагаЯоИіОјЖджЕаЁгк
жагаЯоИіОјЖджЕаЁгк![]() ЕФдЊЫиЕФКЭЃЎ
ЕФдЊЫиЕФКЭЃЎ
Шє![]() ЃЌдђНсТлЯдШЛГЩСЂЃЎ
ЃЌдђНсТлЯдШЛГЩСЂЃЎ
Шє![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
гЩЙщФЩМйЩшжЊЃЌ![]() ПЩвдБэЪОЮЊМЏКЯ
ПЩвдБэЪОЮЊМЏКЯ![]() жагаЯоИіОјЖджЕаЁгк
жагаЯоИіОјЖджЕаЁгк![]() ЕФдЊЫиЕФКЭЃЎ
ЕФдЊЫиЕФКЭЃЎ
ЫљвдЃЌЕБ![]() ЪБНсТлвВГЩСЂЃЛ
ЪБНсТлвВГЩСЂЃЛ
гЩгкьГВЈФЧЦѕЪ§СаЪЧЮоНчЕФЃЌ
ЫљвдЃЌШЮвЛИіе§ећЪ§ЖМПЩвдБэЪОГЩМЏКЯ![]() ЕФвЛИігаЯозгМЏжаЫљгадЊЫиЕФКЭЃЎ
ЕФвЛИігаЯозгМЏжаЫљгадЊЫиЕФКЭЃЎ
вђДЫМЏКЯ![]() гжЪЧ
гжЪЧ![]() ЕФЛљЕзМЏЃЎ
ЕФЛљЕзМЏЃЎ