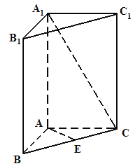
ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΡ≥ΒΊΦΤΜ°‘Ύ“Μ¥ΠΚΘΧ≤Ϋ®‘λ“ΜΗω―χ÷≥≥Γ.
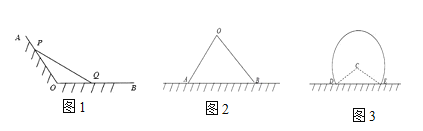
Θ®1Θ©»γΆΦ1Θ§…δœΏOAΘ§OBΈΣΚΘΑΕœΏΘ§![]() Θ§œ÷”Ο≥ΛΕ»ΈΣ1«ßΟΉΒΡΈßΆχPQ“άΆ–ΚΘΑΕœΏΈß≥…“ΜΗω
Θ§œ÷”Ο≥ΛΕ»ΈΣ1«ßΟΉΒΡΈßΆχPQ“άΆ–ΚΘΑΕœΏΈß≥…“ΜΗω![]() ΒΡ―χ÷≥≥ΓΘ§Έ »γΚΈ―Γ»ΓΒψPΘ§QΘ§≤≈Ρή Ι―χ÷≥≥Γ
ΒΡ―χ÷≥≥ΓΘ§Έ »γΚΈ―Γ»ΓΒψPΘ§QΘ§≤≈Ρή Ι―χ÷≥≥Γ![]() ΒΡΟφΜΐΉν¥σΘ§≤Δ«σΤδΉν¥σΟφΜΐ.
ΒΡΟφΜΐΉν¥σΘ§≤Δ«σΤδΉν¥σΟφΜΐ.
Θ®2Θ©»γΆΦ2Θ§÷±œΏlΈΣΚΘΑΕœΏΘ§œ÷”Ο≥ΛΕ»ΈΣ1«ßΟΉΒΡΈßΆχ“άΆ–ΚΘΑΕœΏΈß≥…“ΜΗω―χ÷≥≥Γ.ΖΫΑΗ“ΜΘΚΈß≥…»ΐΫ«–ΈOABΘ®ΒψAΘ§B‘Ύ÷±œΏl…œΘ©Θ§ Ι»ΐΫ«–ΈOABΟφΜΐΉν¥σΘ§…ηΤδΈΣ![]() ΘΜΖΫΑΗΕΰΘΚΈß≥…Ι≠–ΈCDEΘ®ΒψDΘ§E‘Ύ÷±œΏl…œΘ§C «”≈ΜΓΥυ‘Ύ‘≤ΒΡ‘≤–Ρ«“
ΘΜΖΫΑΗΕΰΘΚΈß≥…Ι≠–ΈCDEΘ®ΒψDΘ§E‘Ύ÷±œΏl…œΘ§C «”≈ΜΓΥυ‘Ύ‘≤ΒΡ‘≤–Ρ«“![]() Θ©Θ§ΤδΟφΜΐΈΣ
Θ©Θ§ΤδΟφΜΐΈΣ![]() ΘΜ ‘«σ≥ω
ΘΜ ‘«σ≥ω![]() ΒΡΉν¥σ÷ΒΚΆ
ΒΡΉν¥σ÷ΒΚΆ![]() Θ®ΨυΨΪ»ΖΒΫ0.01ΤΫΖΫ«ßΟΉΘ©Θ§≤Δ÷Η≥ωΡΡ“Μ÷÷…ηΦΤΖΫΑΗΗϋΚΟ.
Θ®ΨυΨΪ»ΖΒΫ0.01ΤΫΖΫ«ßΟΉΘ©Θ§≤Δ÷Η≥ωΡΡ“Μ÷÷…ηΦΤΖΫΑΗΗϋΚΟ.
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() Θ§
Θ§![]() ΤΫΖΫ«ßΟΉΘ®2Θ©
ΤΫΖΫ«ßΟΉΘ®2Θ©![]() ΤΫΖΫ«ßΟΉΘ§
ΤΫΖΫ«ßΟΉΘ§![]() ‘ΦΈΣ0.144ΤΫΖΫ«ßΟΉΘ§ΖΫΑΗΕΰΗϋΚΟ.
‘ΦΈΣ0.144ΤΫΖΫ«ßΟΉΘ§ΖΫΑΗΕΰΗϋΚΟ.
ΓΨΫβΈωΓΩ
Θ®1Θ©…η![]()
![]() Θ§‘ρ
Θ§‘ρ![]() Θ§‘Όάϊ”ΟΜυ±Ψ≤ΜΒ» ΫΒΡ–‘÷ ”κ»ΐΫ«–ΈΟφΜΐΦΤΥψΙΪ ΫΦ¥Ω…ΒΟ≥ω.
Θ§‘Όάϊ”ΟΜυ±Ψ≤ΜΒ» ΫΒΡ–‘÷ ”κ»ΐΫ«–ΈΟφΜΐΦΤΥψΙΪ ΫΦ¥Ω…ΒΟ≥ω.
Θ®2Θ©ΖΫΑΗ“ΜΘΚ…η![]()
![]() Θ§‘ρ
Θ§‘ρ![]() .‘ρ
.‘ρ![]() Θ§άϊ”ΟΜυ±Ψ≤ΜΒ» ΫΒΡ–‘÷ Φ¥Ω…ΒΟ≥ωΉν¥σ÷Β.
Θ§άϊ”ΟΜυ±Ψ≤ΜΒ» ΫΒΡ–‘÷ Φ¥Ω…ΒΟ≥ωΉν¥σ÷Β.
ΖΫΑΗΕΰΘΚ…ηΑκΨΕ![]()
![]() Θ§‘ρ
Θ§‘ρ![]() .ΫβΒΟ
.ΫβΒΟ![]() .
.
Ω…ΒΟ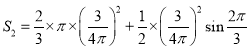 Θ§Φ¥Ω…±»Ϋœ≥ω
Θ§Φ¥Ω…±»Ϋœ≥ω![]() ”κ
”κ![]() ΒΡ¥σ–ΓΙΊœΒ.
ΒΡ¥σ–ΓΙΊœΒ.
ΫβΘΚΘ®1Θ©…η![]()
![]() Θ§
Θ§
‘ρ![]() Θ§
Θ§
Ω…ΒΟ![]() Θ§
Θ§
Β±«“ΫωΒ±![]() ±»ΓΒ»Κ≈.
±»ΓΒ»Κ≈.
![]()
![]() .
.
![]() Β±«“ΫωΒ±
Β±«“ΫωΒ±![]() ±Θ§
±Θ§
―χ÷≥≥Γ![]() ΒΡΟφΜΐΉν¥σΘ§
ΒΡΟφΜΐΉν¥σΘ§![]() Θ®ΤΫΖΫ«ßΟΉΘ©
Θ®ΤΫΖΫ«ßΟΉΘ©
Θ®2Θ©ΖΫΑΗ“ΜΘΚ…η![]()
![]() Θ§
Θ§
‘ρ![]() .
.
‘ρ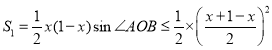
![]() Θ§
Θ§
Β±«“ΫωΒ±![]() ±»ΓΒ»Κ≈.
±»ΓΒ»Κ≈.
![]() Θ®ΤΫΖΫ«ßΟΉΘ©Θ§
Θ®ΤΫΖΫ«ßΟΉΘ©Θ§
ΖΫΑΗΕΰΘΚ…ηΑκΨΕ![]()
![]() Θ§
Θ§
‘ρ![]() .ΫβΒΟ
.ΫβΒΟ![]() .
.
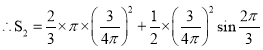
![]() Θ®ΤΫΖΫ«ßΟΉΘ©
Θ®ΤΫΖΫ«ßΟΉΘ©
![]() Θ§ΖΫΑΗΕΰΥυΈß≥…ΒΡ―χ÷≥≥ΓΟφΜΐΫœ¥σΘ§ΖΫΑΗΕΰΗϋΚΟ.
Θ§ΖΫΑΗΕΰΥυΈß≥…ΒΡ―χ÷≥≥ΓΟφΜΐΫœ¥σΘ§ΖΫΑΗΕΰΗϋΚΟ.

 ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ
ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ –Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
–Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ