Ő‚ńŅńŕ»›
°ĺŐ‚ńŅ°Ņő™ŃňĻńņÝ÷į‘ĪĻ§◊ų»»«ť£¨ń≥Ļęňĺ∂‘√ŅőĽ÷į‘Ī“ĽńÍņīĶńĻ§◊ų“Ķľ®įī‘¬ĹÝ––Ņľ∆ņīÚ∑÷£ĽńÍ÷’įī’’÷į‘ĪĶń‘¬∆Ĺĺý÷Ķ∆ņ—°Ļęňĺ◊Óľ—÷į‘Ī≤ʳݔŤŌŗ”¶ĹĪņÝ.“—÷™÷į‘Ī![]() “ĽńÍņīĶńĻ§◊ų“Ķľ®∑÷ żĶńĺ•“∂Õľ»ÁÕľňý ĺ£ļ
“ĽńÍņīĶńĻ§◊ų“Ķľ®∑÷ żĶńĺ•“∂Õľ»ÁÕľňý ĺ£ļ
£®1£©łýĺ›÷į‘Ī![]() Ķń“Ķľ®ĺ•“∂Õľ«ů≥ŲňŻ’‚“ĽńÍĶńĻ§◊ų“Ķľ®Ķń÷–őĽ żļÕ∆Ĺĺý ż£Ľ
Ķń“Ķľ®ĺ•“∂Õľ«ů≥ŲňŻ’‚“ĽńÍĶńĻ§◊ų“Ķľ®Ķń÷–őĽ żļÕ∆Ĺĺý ż£Ľ
£®2£©»Űľ«÷į‘Ī![]() ĶńĻ§◊ų“Ķľ®Ķń‘¬∆Ĺĺý żő™
ĶńĻ§◊ų“Ķľ®Ķń‘¬∆Ĺĺý żő™![]() .
.
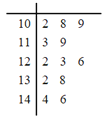
ĘŔ“—÷™ł√ĻęňĺĽĻ”–6őĽ÷į‘ĪĶń“Ķľ®‘ŕ100“‘…Ō£¨∑÷Īū «![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨‘ŕ’‚6»ňĶń“Ķľ®ņÔňśĽķ≥ť»°2łŲ żĺ›£¨«ů«°”–1łŲ żĺ›¬ķ◊„
£¨‘ŕ’‚6»ňĶń“Ķľ®ņÔňśĽķ≥ť»°2łŲ żĺ›£¨«ů«°”–1łŲ żĺ›¬ķ◊„![]() £®∆š÷–
£®∆š÷–![]() £©ĶńłŇ¬ £Ľ
£©ĶńłŇ¬ £Ľ
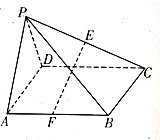
Ęŕ”…”ŕ÷į‘Ī![]() Ķń“Ķľ®łŖ£¨ĪĽĻęňĺ∆ņő™ńÍ∂»◊Óľ—÷į‘Ī£¨‘ŕĻęňĺńÍĽŠ…ŌÕ®Ļż≥ťĹĪ–ő ĹŃž»°ĹĪĹū.Ļęňĺ◊ľĪłŃň9’ŇŅ®∆¨£¨∆š÷–”–1’ŇŅ®∆¨…ŌĪÍ◊ĘĹĪĹūő™6«ß‘™£¨4’ŇŅ®∆¨ĶńĹĪĹūő™4«ß‘™£¨ŃŪÕ‚4’ŇĶńĹĪĹūő™2«ß‘™.Ļś‘Ú «£ļĽŮĹĪ÷į‘Ī–Ť“™ī”9’ŇŅ®∆¨÷–ňśĽķ≥ť≥Ų3’Ň£¨’‚3’ŇŅ®∆¨…ŌĶńĹū∂Ó ż÷ģļÕĺÕ «ł√÷į‘ĪňýĶ√ĹĪĹū.ľ«÷į‘Ī
Ķń“Ķľ®łŖ£¨ĪĽĻęňĺ∆ņő™ńÍ∂»◊Óľ—÷į‘Ī£¨‘ŕĻęňĺńÍĽŠ…ŌÕ®Ļż≥ťĹĪ–ő ĹŃž»°ĹĪĹū.Ļęňĺ◊ľĪłŃň9’ŇŅ®∆¨£¨∆š÷–”–1’ŇŅ®∆¨…ŌĪÍ◊ĘĹĪĹūő™6«ß‘™£¨4’ŇŅ®∆¨ĶńĹĪĹūő™4«ß‘™£¨ŃŪÕ‚4’ŇĶńĹĪĹūő™2«ß‘™.Ļś‘Ú «£ļĽŮĹĪ÷į‘Ī–Ť“™ī”9’ŇŅ®∆¨÷–ňśĽķ≥ť≥Ų3’Ň£¨’‚3’ŇŅ®∆¨…ŌĶńĹū∂Ó ż÷ģļÕĺÕ «ł√÷į‘ĪňýĶ√ĹĪĹū.ľ«÷į‘Ī![]() ĽŮĶ√ĶńĹĪĹūő™
ĽŮĶ√ĶńĹĪĹūő™![]() £®«ß‘™£©£¨«ů
£®«ß‘™£©£¨«ů![]() Ķń∑÷≤ľŃ–ļÕ∆ŕÕŻ.
Ķń∑÷≤ľŃ–ļÕ∆ŕÕŻ.
°ĺīūįł°Ņ£®1£©÷–őĽ ż «![]() £Ľ∆Ĺĺý ż «
£Ľ∆Ĺĺý ż «![]() £®2£©ĘŔ
£®2£©ĘŔ![]() ĘŕŌÍľŻĹ‚őŲ
ĘŕŌÍľŻĹ‚őŲ
°ĺĹ‚őŲ°Ņ
£®1£©÷ĪĹ”ņŻ”√÷–őĽ żļÕ∆Ĺĺý żĶńłŇńÓĻę Ĺņīľ∆ň„ľīŅ…£Ľ
£®2£©ĘŔ’“≥Ų∑ŻļŌŐűľĢĶń żĺ›£¨ņŻ”√ĻŇĶšłŇ–ÕĻę Ĺ«ů≥ŲłŇ¬ ľīŅ….
Ęŕ”…Ő‚“‚÷™![]() ňý”–»°÷Ķő™£ļ6£¨8£¨10£¨12£¨14£¨ņŻ”√ĻŇĶšłŇ–ÕĻę Ĺ«ů≥ŲłŇ¬ £¨ĹÝ∂ÝŅ…Ķ√∑÷≤ľŃ–ļÕ∆ŕÕŻ.
ňý”–»°÷Ķő™£ļ6£¨8£¨10£¨12£¨14£¨ņŻ”√ĻŇĶšłŇ–ÕĻę Ĺ«ů≥ŲłŇ¬ £¨ĹÝ∂ÝŅ…Ķ√∑÷≤ľŃ–ļÕ∆ŕÕŻ.
Ĺ‚£ļ£®1£©”…ĺ•“∂ÕľŅ…÷™£¨ňý«ůĶń÷–őĽ ż «![]() £Ľ
£Ľ
∆Ĺĺý ż «![]() £Ľ
£Ľ
£®2£©ĘŔ”…£®1£©÷™![]() £¨ĘŔ¬ķ◊„
£¨ĘŔ¬ķ◊„![]() Ķń”–
Ķń”–![]() £¨
£¨![]() £¨
£¨
ňý“‘£¨ňý«ůĶńłŇ¬ ![]() £Ľ
£Ľ
Ęŕ”…Ő‚“‚÷™![]() ňý”–»°÷Ķő™£ļ6£¨8£¨10£¨12£¨14‘Ú
ňý”–»°÷Ķő™£ļ6£¨8£¨10£¨12£¨14‘Ú
![]() £Ľ
£Ľ
![]() £Ľ
£Ľ
![]() £Ľ
£Ľ
![]() £Ľ
£Ľ
![]() .
.
ňý“‘![]() Ķń∑÷≤ľŃ–ő™
Ķń∑÷≤ľŃ–ő™
| 6 | 8 | 10 | 12 | 14 |
|
|
|
|
|
|
ňý“‘£¨∆ŕÕŻ![]() £®«ß‘™£©.
£®«ß‘™£©.