题目内容
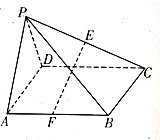
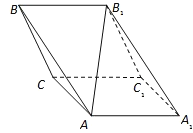
【题目】斜三棱柱ABC﹣A1B1C1,已知侧面BB1C1C与底面ABC垂直且∠BCA=90°,∠B1BC=60°,BC=BB1=2,若二面角A﹣B1B﹣C为30°
(1)求AB1与平面BB1C1C所成角的正切值;
(2)在平面AA1B1B内找一点P,使三棱锥P﹣BB1C为正三棱锥,并求P到平面BB1C距离.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)由侧面BB1C1C与底面ABC垂直且∠BCA=90°知AC⊥平面BB1C1C,则有∠AB1C为AB1与平面BB1C1C所成的角,连接B1C,则∠AB1C为AB1与平面BB1C1C所成的角,在Rt△ACB1中可求得tan∠AB1C.
(2)在AD上取点P,使AP=2PD,则P点为所求,在CD上取点O,使CO=2OD,连PO,则易知三棱锥P﹣BB1C为正三棱锥,故可求.
(1)由侧面BB1C1C与底面ABC垂直且∠BCA=90°知AC⊥平面BB1C1C,
取BB1的中点D,AC⊥平面BB1C1C,
∴AC⊥BB1,
∴BB1⊥平面ADC,
∴AD⊥BB1,
∴∠CDA为二面角A﹣BB1﹣C的平面角,∴∠CDA=30°,
∵CD=![]() ,∴AC=1,
,∴AC=1,
连接B1C,则∠AB1C为AB1与平面BB1C1C所成的角,
在Rt△ACB1中tan∠AB1C=![]() ,
,
(2)在AD上取点P,使AP=2PD,则P点为所求,
在CD上取点O,使CO=2OD,连PO,
则PO∥AC,且PO=![]() ,
,
∵AO⊥平面BB1C,
∴PO⊥平面BB1C 且 BB1C为等边三角形,
∴三棱锥P﹣BB1C为正三棱锥,
且P到平面BB1C的距离为PO,PO=![]() .
.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目