题目内容
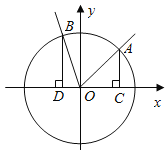
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,过左焦点
,过左焦点![]() 的直线与椭圆交于
的直线与椭圆交于![]() ,
,![]() 两点,且线段
两点,且线段![]() 的中点为
的中点为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() 为
为![]() 上一个动点,过点
上一个动点,过点![]() 与椭圆
与椭圆![]() 只有一个公共点的直线为
只有一个公共点的直线为![]() ,过点
,过点![]() 与
与![]() 垂直的直线为
垂直的直线为![]() ,求证:
,求证:![]() 与
与![]() 的交点在定直线上,并求出该定直线的方程.
的交点在定直线上,并求出该定直线的方程.
【答案】(Ⅰ)![]() ;(Ⅱ)证明见解析,
;(Ⅱ)证明见解析,![]() ,
,
【解析】
(Ⅰ)设![]() ,
,![]() ,根据点
,根据点![]() ,
,![]() 都在椭圆上,代入椭圆方程两式相减,根据“设而不求”的思想,结合离心率以及中点坐标公式、直线的斜率建立等式即可求解.
都在椭圆上,代入椭圆方程两式相减,根据“设而不求”的思想,结合离心率以及中点坐标公式、直线的斜率建立等式即可求解.
(Ⅱ)设![]() ,由对称性,设
,由对称性,设![]() ,由
,由![]() ,得椭圆上半部分的方程为
,得椭圆上半部分的方程为![]() ,从而求出直线
,从而求出直线![]() 的方程,再由过点
的方程,再由过点![]() 与
与![]() 垂直的直线为
垂直的直线为![]() ,求出
,求出![]() ,两方程联立,消去
,两方程联立,消去![]() ,即可求解.
,即可求解.
(Ⅰ)由题可知![]() ,直线
,直线![]() 的斜率存在.
的斜率存在.
设![]() ,
,![]() ,由于点
,由于点![]() ,
,![]() 都在椭圆上,
都在椭圆上,
所以![]() ①,
①,![]() ②,
②,
①-②,化简得![]() ③
③
又因为离心率为![]() ,所以
,所以![]() .
.
又因为直线![]() 过焦点
过焦点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,
,
所以![]() ,
,![]() ,
, ,
,
代入③式,得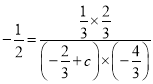 ,解得
,解得![]() .
.
再结合![]() ,解得
,解得![]() ,
,![]() ,
,
故所求椭圆的方程为![]() .
.
(Ⅱ)证明:设![]() ,由对称性,设
,由对称性,设![]() ,由
,由![]() ,得椭圆上半部分的方程为
,得椭圆上半部分的方程为![]() ,
, ,
,
又![]() 过点
过点![]() 且与椭圆只有一个公共点,所以
且与椭圆只有一个公共点,所以![]() ,
,
所以![]() :
:![]() ,④
,④
因为![]() 过点
过点![]() 且与
且与![]() 垂直,所以
垂直,所以![]() :
:![]() ,⑤
,⑤
联立④⑤,消去![]() ,得
,得![]() ,
,
又![]() ,所以
,所以![]() ,从而可得
,从而可得![]() ,
,
所以![]() 与
与![]() 的交点在定直线
的交点在定直线![]() 上.
上.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目