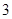题目内容
设函数f(x)=
(a,b∈Z+)满足f(1)=2,f(2)<3.
(1)求a,b的值;
(2)当x≥
时,求出f(x)的值域.
| ax2+1 |
| bx |
(1)求a,b的值;
(2)当x≥
| 1 |
| 2 |
(1)∵f(1)=1,f(2)<3,
∴
,
化简可得
,
故有
<0,
∴0<b<
.
又a,b∈Z,∴a=b=1.
(2)由(1)得 f(x)=x+
,当x≥
时,
利用基本不等式可得f(x)≥2,当且仅当x=1时取等号,
故当x≥
时,f(x)的值域为[2,+∞).
∴
|
化简可得
|
故有
| 2b-3 |
| 2b |
∴0<b<
| 3 |
| 2 |
又a,b∈Z,∴a=b=1.
(2)由(1)得 f(x)=x+
| 1 |
| x |
| 1 |
| 2 |
利用基本不等式可得f(x)≥2,当且仅当x=1时取等号,
故当x≥
| 1 |
| 2 |

练习册系列答案
相关题目

 ,
, 满足约束条件
满足约束条件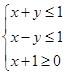 ,则
,则 的最小值为( )
的最小值为( )