题目内容
17．计算：（xnex）′=nxn-1ex+xnex．分析 结合题意由乘积的导数可得答案．
解答 解：由乘积的导数可得：
（xnex）′=（xn）′ex+xn（ex）′
=nxn-1ex+xnex
故答案为：nxn-1ex+xnex
点评 本题考查导数的运算，属基础题．
练习册系列答案
相关题目
7．下列各组中的两个函数是相同函数的为（ ）
| A． | f（x）=$\frac{（x+3）（x-5）}{x+3}$，g（x）=x-5 | B． | f（x）=x，g（x）=$\sqrt{x^2}$ | ||
| C． | f（x）=x，g（x）=$\root{3}{x^3}$ | D． | f（x）=$\sqrt{x+1}\sqrt{x-1}$，g（x）=$\sqrt{（x+1）（x-1）}$ |
8．有下列四个命题，其中真命题有：
①“若x+y=0，则x、y互为相反数”的逆命题
②“全等三角形的面积相等”的否命题
③“若q≤1，则x2+2x+q=0有实根”的逆命题
④“不等边三角形的三个内角相等”的逆否命题，其中真命题的序号为（ ）
①“若x+y=0，则x、y互为相反数”的逆命题
②“全等三角形的面积相等”的否命题
③“若q≤1，则x2+2x+q=0有实根”的逆命题
④“不等边三角形的三个内角相等”的逆否命题，其中真命题的序号为（ ）
| A． | ①③ | B． | ②③ | C． | ①② | D． | ③④ |
5．函数y=sin（ωx+φ）的部分图象如图，则f（$\frac{π}{2}$）=（ ）
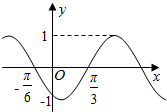
| A． | -$\frac{1}{2}$ | B． | $\frac{1}{2}$ | C． | -$\frac{\sqrt{3}}{2}$ | D． | $\frac{\sqrt{3}}{2}$ |
已知圆N：（x+1）2+y2=2的切线l与抛物线C：y2=x交于不同的两点A，B．
如图，摩天轮的半径OA为50m，它的最低点A距地面的高度忽略不计．地面上有一长度为240m的景观带MN，它与摩天轮在同一竖直平面内，且AM=60m．点P从最低点A处按逆时针方向转动到最高点B处，记∠AOP=θ，θ∈（0，π）．