Question

5．函数y=sin（ωx+φ）的部分图象如图，则f（$\frac{π}{2}$）=（　　）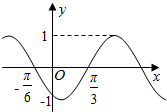

• A． -$\frac{1}{2}$
• B． $\frac{1}{2}$
• C． -$\frac{\sqrt{3}}{2}$
• D． $\frac{\sqrt{3}}{2}$

Answer 1

分析 通过函数的图象，求出T然后求出ω，利用图象经过（$\frac{π}{3}$，0），求出φ的值，解得函数解析式，即可求值．

解答 解：由题意可知：T=2（$\frac{π}{3}$+$\frac{π}{6}$）=π，所以ω=$\frac{2π}{T}$=2，
因为函数经过（$\frac{π}{3}$，0），所以 0=sin（2×$\frac{π}{3}$+φ），所以φ=2kπ-$\frac{2π}{3}$，k∈Z，
则：f（$\frac{π}{2}$）=sin（2×$\frac{π}{2}$+2kπ-$\frac{2π}{3}$）=sin（$\frac{π}{3}$+2kπ）=$\frac{\sqrt{3}}{2}$．
故选：D．

点评 本题是基础题，考查三角函数的图象的应用，学生的视图能力，注意角的范围的应用．