题目内容
7.已知函数f(x)=$\left\{\begin{array}{l}{(\frac{1}{2})^{x}+\frac{3}{4},}&{x≥2}\\{lo{g}_{2}x,}&{0<x<2}\end{array}\right.$,若关于x的方程f(x)-k=0有且只有1个根,则实数k的取值范围是k≤$\frac{3}{4}$或k=1.分析 由题意可得函数f(x)的图象与直线y=k有1个不同的交点,结合图象求出实数k的取值范围.
解答 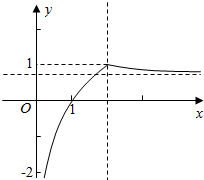 解:①当x≥2时,f(x)在[2,+∞)上单调递减,且$\frac{3}{4}$<f(x)≤1;
解:①当x≥2时,f(x)在[2,+∞)上单调递减,且$\frac{3}{4}$<f(x)≤1;
②当0<x<2时,f(x)在(0,2)上单调递增,且f(x)<1;
由g(x)=f(x)-k有且只有1个根可化为y=f(x)与y=k的1个交点,
则k≤$\frac{3}{4}$或k=1.
故答案为:k≤$\frac{3}{4}$或k=1.
点评 本题主要考查函数的零点与方程的根的关系,体现了化归与转化、数形结合的数学思想,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.设函数f(x)=$\left\{\begin{array}{l}{{2}^{x}-a,}&{x<1}\\{4(x-a)(x-2a),}&{x≥1}\end{array}\right.$,若f(x)恰有2个零点,则实数a的取值范围是( )
| A. | a≥2 | B. | $\frac{1}{2}$≤a<1 | C. | $\frac{1}{2}$<a<1 | D. | a≥2或$\frac{1}{2}$≤a<1 |
19.如果f(x)=$\frac{1}{2}$(m-2)x2+(n-8)x+1(m>2,n>0)在[$\frac{1}{2},2$]上单调递减,则$\frac{1}{m}$+$\frac{1}{n}$的最小值为( )
| A. | $\frac{\sqrt{2}}{3}$ | B. | $\frac{\sqrt{2}}{6}$ | C. | $\frac{3+2\sqrt{2}}{12}$ | D. | $\frac{3-2\sqrt{2}}{12}$ |
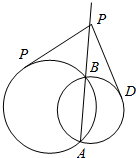 如图,两圆相交于A、B两点,P为两圆公共弦AB上任一点,从P引两圆的切线PC、PD,若PC=2$\sqrt{2}$cm,则PD=2$\sqrt{2}$cm.
如图,两圆相交于A、B两点,P为两圆公共弦AB上任一点,从P引两圆的切线PC、PD,若PC=2$\sqrt{2}$cm,则PD=2$\sqrt{2}$cm.