Question

【题目】在直角坐标系 中，直线 的参数方程为 为参数），以该直角坐标系的原点 为极点， 轴的非负半轴为极轴的极坐标系下，圆 的方程为 ．
（1）求直线 的普通方程和圆 的圆心的极坐标；
（2）设直线 和圆 的交点为 、 ，求弦 的长．

Answer 1

【答案】
（1）解：由 的参数方程消去参数 得普通方程为

圆 的直角坐标方程 ,

所以圆心的直角坐标为 ，因此圆心的一个极坐标为 .

(答案不唯一，只要符合要求即可)

（2）解：由（1）知圆心 到直线 的距离 ,

所以 .

【解析】分析：本题主要考查了直线的参数方程，解决问题的关键是（1）消去参数即可将 的参数方程化为普通方程，在直角坐标系下求出圆心的坐标，化为极坐标即可；（2）求出圆心到直线的距离，由勾股定理求弦长即可
【考点精析】关于本题考查的直线的参数方程，需要了解经过点，倾斜角为的直线的参数方程可表示为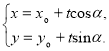（为参数）才能得出正确答案．