题目内容
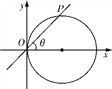
【题目】将圆x2+y2=1 每一点的，横坐标保持不变，纵坐标变为原来的2倍，得到曲线C．
（1）写出C的参数方程；
（2）设直线l:2x+y-2=0 与C的交点为P1,P2 ，以坐标原点为极点， x 轴的正半轴为极轴建立极坐标系，求线段 P1P2 的中点且与 l 垂直的直线的极坐标方程．
【答案】
（1）
解：设（x1，y1）为圆上的点，在已知变换下变为C上点（x，y），依题意，得
由x12＋y12＝1得
，即曲线C的方程为
.
故C的参数方程为
（t为参数）．
（2）
解：由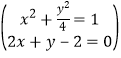
，解得
或
不妨设P1（1，0），P2（0，2），则线段P1P2的中点坐标为
，所求直线的斜率
，于是所求直线方程为
,
化为极坐标方程，并整理得
2ρcos θ－4ρsin θ＝－3，即
.
【解析】本题主要考查了椭圆的参数方程，决问题的关键是（1）在曲线C上任取一点（x,y) ，可以根据点
在圆 x2+y2=1 上，求出C的方程，再化为参数方程；（2）解方程组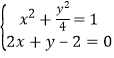
求得P1,P2 的坐标，可得线段 P1P2 的中点坐标，再根据与直线 l 垂直的直线的斜率为，用点斜式求得直线方程，并利用 
将其化为极坐标方程.
【考点精析】本题主要考查了椭圆的参数方程的相关知识点，需要掌握椭圆
的参数方程可表示为
才能正确解答此题．
名校课堂系列答案【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比，收获时各随机抽取了100个网箱，测量各箱水产品的产量（单位：kg）, 其频率分布直方图如下：
（1）记A表示事件“旧养殖法的箱产量低于50 kg”，估计A的概率；
（2）填写下面列联表，并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关：
箱产量＜50 kg | 箱产量≥50 kg | |
旧养殖法 | ||
新养殖法 |
（3）根据箱产量的频率分布直方图，对这两种养殖方法的优劣进行比较.
附：
P（ | 0.050 0.010 0.001 |
k | 3.841 6.635 10.828 |
. 
【题目】随机询问某大学40名不同性别的大学生在购买食物时是否读营养说明，得到如下列联表：
男 | 女 | 总计 | |
读营养说明 | 16 | 8 | 24 |
不读营养说明 | 4 | 12 | 16 |
总计 | 20 | 20 | 40 |
（1）根据以上列联表进行独立性检验，能否在犯错误的概率不超过0.01的前提下认为性别与是否读营养说明之间有关系？
（2）从被询问的16名不读营养说明的大学生中，随机抽取2名学生，求抽到男生人数
的分布列及其均值（即数学期望）．
（注： 
，其中
为样本容量）
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
