题目内容
4.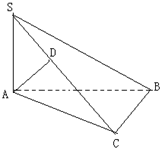 已知在三棱锥S-ABC中,∠ACB=90°,又SA⊥平面ABC,AD⊥SC于D,求证:
已知在三棱锥S-ABC中,∠ACB=90°,又SA⊥平面ABC,AD⊥SC于D,求证:(1)面SAC⊥面SBC
(2)AD⊥平面SBC.
分析 (1)运用线面垂直的性质和判定,可得BC⊥平面SAC,即有BC⊥AD,AD⊥SC,则AD⊥平面SBC,再由面面垂直的判定定理,即可得证;
(2)运用面面垂直的性质定理,即可得证.
解答 证明:(1)SA⊥平面ABC,
即有SA⊥BC,
又BC⊥AC,
可得BC⊥平面SAC,
即有BC⊥AD,AD⊥SC,
则AD⊥平面SBC,
AD?平面SAC,
则平面SAC⊥平面SBC;
(2)由(1)可得,平面SAC⊥平面SBC,
AD⊥SC于D,
由面面垂直的性质定理可得,
AD⊥平面SBC.
点评 本题考查空间线面垂直的判定和性质定理的运用,考查空间想象能力和推理能力,属于中档题.

练习册系列答案
相关题目
15.若集合C={m|函数y=x2+(m-2)x+2为偶函数},集合D={y|y=$\frac{x}{x-1}$,2≤x≤3}.则C∩D=( )
| A. | ϕ | B. | {1} | C. | {2} | D. | [$\frac{3}{2}$,2] |
9.某单位有20名职工,将其编号为01~20,现用随机数表从中抽取5名职工进行座谈会,若抽取的第一名职工的编号是如下随机数表中的第一行,第5列和第6列,则抽取的第5名职工的编号为( )

| A. | 17 | B. | 13 | C. | 03 | D. | 04 |
16.“x>1”是“x(x-1)>0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |