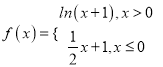题目内容
【题目】如图,我国南海某处的一个圆形海域上有四个小岛,小岛B与小岛A、小岛C相距都为5n mile,与小岛D相距为 ![]() n mile.小岛A对小岛B与D的视角为钝角,且
n mile.小岛A对小岛B与D的视角为钝角,且 ![]() .
.
(Ⅰ)求小岛A与小岛D之间的距离和四个小岛所形成的四边形的面积;
(Ⅱ)记小岛D对小岛B与C的视角为α,小岛B对小岛C与D的视角为β,求sin(2α+β)的值.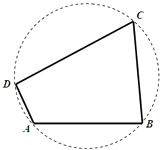
【答案】解:(Ⅰ)∵ ![]() ,且角A为钝角,∴
,且角A为钝角,∴ 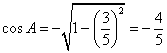 .
.
在△ABD中,由余弦定理得:AD2+AB2﹣2ADABcosA=BD2 .
∴ ![]() AD2+8AD﹣20=0.
AD2+8AD﹣20=0.
解得AD=2或AD=﹣10(舍).
∴小岛A与小岛D之间的距离为2n mile.
∵A,B,C,D四点共圆,∴角A与角C互补.
∴ ![]() ,
, ![]() .
.
在△BDC中,由余弦定理得:CD2+CB2﹣2CDCBcosC=BD2 .
∴ ![]() CD2﹣8CD﹣20=0.
CD2﹣8CD﹣20=0.
解得CD=﹣2(舍)或CD=10
∴S四边形ABCD=S△ABC+S△BCD
= ![]() =
= ![]() =3+15=18.
=3+15=18.
∴四个小岛所形成的四边形的面积为18平方n mile.
(Ⅱ)在△BDC中,由正弦定理得: ![]()
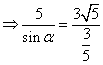
![]() .
.
∵DC2+DB2>BC2 , ∴α为锐角,∴ ![]() .
.
又∵ ![]() ,
, ![]() .
.
∴sin(2α+β)=sin[α+(α+β)]
=sinαcos(α+β)+cosαsin(α+β)=sinαcos(α+β)+cosαsin(α+β)
= ![]() =
= ![]()
【解析】(Ⅰ)利用余弦定理求出,AD,CD,即可求小岛A与小岛D之间的距离和四个小岛所形成的四边形的面积;(Ⅱ)求出sin(α+β),cos(α+β),利用和角的三角函数公式求sin(2α+β)的值.

 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案【题目】一企业从某生产线上随机抽取40件产品,测量这些产品的某项技术指标值![]() ,得到如下的频数表
,得到如下的频数表
|
|
|
|
|
频数 | 3 | 15 | 17 | 5 |
(1)估计该技术指标值的平均数(以各组区间中点值为代表);
(2)若![]() ,则该产品不合格,其余合格产品。产生一件产品,若是合格品,可盈利100元,若不是合格品则亏损20元。从该生产线生产的产品中任取2件,记
,则该产品不合格,其余合格产品。产生一件产品,若是合格品,可盈利100元,若不是合格品则亏损20元。从该生产线生产的产品中任取2件,记![]() 为这2件产品的总利润,求随机变量
为这2件产品的总利润,求随机变量![]() 的分布列和期望值。
的分布列和期望值。