题目内容
9.将函数y=sin(2x+φ)的图象沿x轴向左平移$\frac{π}{8}$个单位后,得到函数f(x)的图象,且满足f(x)=f(-x),则φ的一个可能取值为( )| A. | $\frac{3π}{4}$ | B. | $\frac{π}{4}$ | C. | 0 | D. | -$\frac{π}{4}$ |
分析 由题意利用函数y=Asin(ωx+φ)的图象变换规律,可得f(x)=sin(2x+$\frac{π}{4}$+φ),再根据f(x)为偶函数,$\frac{π}{4}$+φ=kπ+$\frac{π}{2}$,k∈z,可得φ的一个可能取值.
解答 解:将函数y=sin(2x+φ)的图象沿x轴向左平移$\frac{π}{8}$个单位后,得到函数f(x)=sin[2(x+$\frac{π}{8}$)+φ]=sin(2x+$\frac{π}{4}$+φ) 的图象,
再根据f(x)=f(-x),可得f(x)为偶函数,故$\frac{π}{4}$+φ=kπ+$\frac{π}{2}$,k∈z,则φ的一个可能取值为$\frac{π}{4}$,
故选:B.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,正弦函数、余弦函数的奇偶性,属于基础题.

练习册系列答案
相关题目
19.若α+β=$\frac{π}{4}$,则(tanα+1)•(tanβ+1)=( )
| A. | 1 | B. | 2 | C. | 3 | D. | 6 |
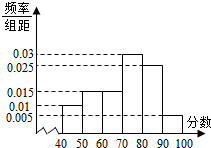 从参加环保竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如图所示,观察图形,回答下列问题:
从参加环保竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如图所示,观察图形,回答下列问题: