题目内容
17.若满足条件C=30°,AB=2,BC=a的△ABC有两个,那么a的取值范围是( )| A. | (1,2) | B. | (1,2$\sqrt{3}$) | C. | (2,4) | D. | (2,4$\sqrt{3}$) |
分析 由已知条件C的度数,AB及BC的值,根据正弦定理用a表示出sinA,由C的度数及正弦函数的图象可知满足题意△ABC有两个A的范围,然后根据A的范围,利用特殊角的三角函数值即可求出sinA的范围,进而求出a的取值范围.
解答 解:∵C=30°,AB=2,BC=a,
∴由正弦定理得:$\frac{AB}{sinC}=\frac{BC}{sinA}$,即 $\frac{2}{\frac{1}{2}}$=$\frac{a}{sinA}$=4,
解得:sinA=$\frac{a}{4}$,
由题意得:当sinA∈($\frac{1}{2}$,1)时,满足条件的△ABC有两个,
解得:2<a<4,
则a的取值范围是(2,4).
故选:C.
点评 此题属于解三角形的题型,涉及的知识有:正弦定理,正弦函数的图象与性质,以及特殊角的三角函数值,熟练掌握正弦定理是解本题的关键.

练习册系列答案
相关题目
7.设A是整数集的一个非空子集,对于k∈A,如果k-1∉A且k+1∉A,那么k是A的一个“孤立元”,给定S={1,2,3,4,5,6,7,8},由S的3个元素构成的所有集合中,不含“孤立元”的 集合共有( ) 个.
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
8.已知tanα=2,则sinαcosα=( )
| A. | -$\frac{2}{3}$ | B. | $\frac{2}{5}$ | C. | -$\frac{4}{5}$ | D. | $\frac{4}{5}$ |
12.函数y=sin(ωx+φ)(ω>0且|φ<|$\frac{π}{2}$)在区间[$\frac{1}{12}$,$\frac{7}{12}$]上单调递减,且函数值从1减小到-1,那么此函数图象与y轴交点的纵坐标为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{6}+\sqrt{2}}{4}$ |
9.某市调研考试后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于120分为优秀,120分以下为非优秀.统计成绩后,得到如下的2×2列联表
(Ⅰ)根据列联表的数据,判断是否有99%的把握认为“成绩与班级有关系”;
(Ⅱ)若按下面的方法从甲班优秀的学生中抽取一人:把甲班10名优秀学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号.试求抽到8号的概率.
参考公式与临界值表:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
| 优秀 | 非优秀 | 合计 | |
| 甲班 | 10 | 40 | 50 |
| 乙班 | 20 | 30 | 50 |
| 合计 | 30 | 70 | 100 |
(Ⅱ)若按下面的方法从甲班优秀的学生中抽取一人:把甲班10名优秀学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号.试求抽到8号的概率.
参考公式与临界值表:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
| P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
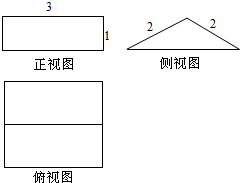 一个几何体的正视图是长为3、宽为1的矩形,侧视图是腰长为2的等腰三角形,则该几何的表面积为12+8$\sqrt{3}$.
一个几何体的正视图是长为3、宽为1的矩形,侧视图是腰长为2的等腰三角形,则该几何的表面积为12+8$\sqrt{3}$.