题目内容
在椭圆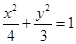 内有一点
内有一点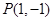 ,
,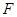 为椭圆的右焦点,在椭圆上有一点
为椭圆的右焦点,在椭圆上有一点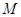 ,
,
使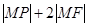 的值最小,则此最小值为 ( )
的值最小,则此最小值为 ( )
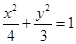 内有一点
内有一点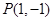 ,
,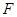 为椭圆的右焦点,在椭圆上有一点
为椭圆的右焦点,在椭圆上有一点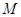 ,
,使
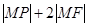 的值最小,则此最小值为 ( )
的值最小,则此最小值为 ( )A. | B. | C. | D. |
B
分析:由题意求出椭圆的离心率,求出焦点坐标,通过椭圆的第二定义,求出|MP|+2|MF|的最小值.
解答:解:由题意作图,
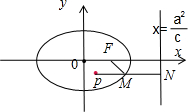
F(1,0),椭圆的离心率为: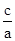 =
=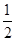 ,
,
由椭圆的第二定义可知,2|MF|=|MN|,如图.
所以|MP|+2|MF|的最小值,就是由P作PN垂直于椭圆的准线于N,
|PN|为所求,
椭圆的右准线方程为x=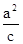 =4,
=4,
所以|MP|+2|MF|的最小值为:4-1=3.
故选B.
解答:解:由题意作图,

F(1,0),椭圆的离心率为:
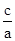 =
=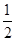 ,
,由椭圆的第二定义可知,2|MF|=|MN|,如图.
所以|MP|+2|MF|的最小值,就是由P作PN垂直于椭圆的准线于N,
|PN|为所求,
椭圆的右准线方程为x=
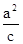 =4,
=4,所以|MP|+2|MF|的最小值为:4-1=3.
故选B.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的左、右焦点分别为
的左、右焦点分别为 、
、 ,
, 是椭圆上一点,
是椭圆上一点,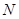 是
是 的中点,若
的中点,若 ,则
,则 的长等于( )
的长等于( )



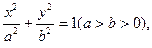 过点A(a,0),B(0,b)的直
过点A(a,0),B(0,b)的直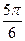 ,原点到该直线的距离为
,原点到该直线的距离为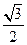 .
.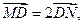 求直线MN的方程;
求直线MN的方程;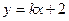 交椭圆于P、Q两点,以PQ为直径的圆过点D(1,0)?若存在,求出k的值;若不存在,请说明理由。
交椭圆于P、Q两点,以PQ为直径的圆过点D(1,0)?若存在,求出k的值;若不存在,请说明理由。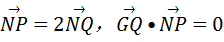 .
.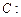
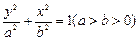 经过点
经过点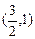 ,一个焦点是
,一个焦点是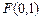 .
.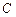 的方程;
的方程;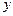 轴的两个交点为
轴的两个交点为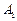 、
、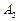 ,不在
,不在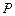 在直线
在直线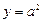 上运动,直线
上运动,直线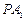 、
、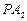 分别与椭圆
分别与椭圆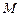 、
、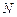 ,证明:直线
,证明:直线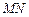 经过焦点
经过焦点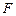 .
.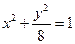 ,射线
,射线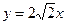 (x≥0)与椭圆的交点为M,过M作倾斜角互补的两条直线,分别与椭圆交于A、B两点(异于M).
(x≥0)与椭圆的交点为M,过M作倾斜角互补的两条直线,分别与椭圆交于A、B两点(异于M).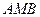 面积的最大值.
面积的最大值. :
: 与抛物线
与抛物线 :
: 的一个交点为M,抛物线
的一个交点为M,抛物线
 ,求
,求

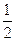
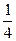
 及椭圆
及椭圆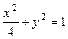 上任意一点
上任意一点 ,则
,则 最大值为 。
最大值为 。