题目内容
【题目】已知点P(2,0),且圆C:x2+y2﹣6x+4y+4=0.
(Ⅰ)当直线![]() 过点P且与圆心C的距离为1时,求直线
过点P且与圆心C的距离为1时,求直线![]() 的方程;
的方程;
(Ⅱ)设过点P的直线与圆C交于A、B两点,若|AB|=4,求以线段AB为直径的圆的方程.
【答案】(1)x=2;(2)(x-2)2+y2=4
【解析】本试题主要是考查了直线与圆的位置关系的运用。以及圆的方程的求解问题。
(1)因为设直线l的斜率为k(k存在)则方程为y-0=k(x-2)
又⊙C的圆心为(3,-2) ,r=3,利用线与圆的位置关系可知直线的方程。
(2)根据设过点P的直线与圆C交于A、B两点,当|AB|=4,利用半径长和半弦长,弦心距的勾股定理得到结论。
解:(1)设直线l的斜率为k(k存在)则方程为y-0=k(x-2) …………………1分
又⊙C的圆心为(3,-2) ,r=3
由![]() ……………………4分
……………………4分
所以直线方程为![]() ……………………6分
……………………6分
当k不存在时,l的方程为x=2. ……………………8分
(2)由弦心距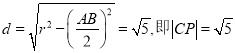 , ……………………11分
, ……………………11分
知P为AB的中点,故以AB为直径的圆的方程为(x-2)2+y2=4. …………………14分

【题目】“奶茶妹妹”对某时间段的奶茶销售量及其价格进行调查,统计出售价![]() 元和销售量
元和销售量![]() 杯之间的一组数据如下表所示:
杯之间的一组数据如下表所示:
价格 | 5 | 5.5 | 6.5 | 7 |
销售量 | 12 | 10 | 6 | 4 |
通过分析,发现销售量![]() 对奶茶的价格
对奶茶的价格![]() 具有线性相关关系.
具有线性相关关系.
(Ⅰ)求销售量![]() 对奶茶的价格
对奶茶的价格![]() 的回归直线方程;
的回归直线方程;
(Ⅱ)欲使销售量为![]() 杯,则价格应定为多少?
杯,则价格应定为多少?
附:线性回归方程为![]() ,其中
,其中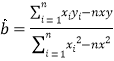 ,
,![]()
【题目】某商店计划每天购进某商品若干件,商店每销售1件该商品可获利50元.若供大于求,剩余商品全部退回,则每件商品亏损10元;若供不应求,则从外部调剂,此时每件调剂商品可获利30元.
(Ⅰ)若商店一天购进该商品10件,求当天的利润y(单位:元)关于当天需求量n(单位:件,n∈N)的函数解析式;
(Ⅱ)商店记录了50天该商品的日需求量(单位:件),整理得下表:
日需求量n | 8 | 9 | 10 | 11 | 12 |
频数 | 10 | 10 | 15 | 10 | 5 |
①假设该店在这50天内每天购进10件该商品,求这50天的日利润(单位:元)的平均数;
②若该店一天购进10件该商品,记“当天的利润在区间![]() ”为事件A,求P(A)的估计值.
”为事件A,求P(A)的估计值.