题目内容

已知椭圆
x2
a2
+
y2
b2
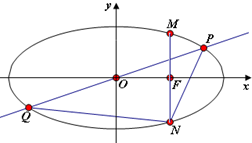
=1(a＞b＞0)的左右焦点为F1（-c，0），F2（c，0），点Q是椭圆外的动点，满足|
F1Q
|=2a，点P是线段F1Q与该椭圆的交点
（1）若点P的横坐标为
a
2
，证明：|
F1P
|=a+
c
2

（2）若存在点Q，使得△F1QF2的面积等于b2，求椭圆离心率的取值范围．
（1）证明：椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)的左准线方程为x=-
a2
c

∵点P的横坐标为
a
2
，
∴由椭圆的定义可知，
|
F1P
|
|
a
2
+
a2
c
|
=
c
a
，
∴|
F1P
|=a+
c
2
；
（2）设Q（x，y），则
∵|
F1Q
|=2a，∴（x+c）2+y2=4a2
∴|y|≤2a
∵存在点Q，使得△F1QF2的面积等于b2，
∴
1
2
•2c•|y|=b2
∴|y|=
b2
c

∴
b2
c
≤2a
∴e2+2e-1≥0
∴e≥
2
-1或e≤-
2
-1
∵0＜e＜1
∴
2
-1≤e＜1．
练习册系列答案
相关题目
如图，椭圆E：
x2
a2
+
y2
b2
=1(a＞b＞0)的右焦点F2与抛物线y2=4x的焦点重合，过F2作与x轴垂直的直线l与椭圆交于S、T两点，与抛物线交于C、D两点，且
|CD|
|ST|
=2
2
．
（Ⅰ）求椭圆E的方程；
（Ⅱ）若过点M（2，0）的直线与椭圆E相交于两点A，B，设P为椭圆E上一点，且满足
OA
+
OB
=t
OP
（O为坐标原点），当|
PA
-
PB
|＜
2
5
3
时，求实数t的取值范围．
已知双曲线C：
x2
a2
-
y2
b2
=1(a＞0，b＞0)的渐近线方程为y=±
3
x，O为坐标原点，点M(
5
，
3
)在双曲线上．
（1）求双曲线C的方程；
（2）若直线l与双曲线交于P，Q两点，且
OP
⊥
OQ
，求|OP|2+|OQ|2的最小值．
已知椭圆的中心在坐标原点，焦点F1、F2在x轴上，长轴A1A2的长为4，左准线l与x轴的交点为M，
MA1
=2
A1F1
．
（I）求椭圆的标准方程；
（Ⅱ）过点M的直线l'与椭圆交于C、D两点，若
OC
•
OD
=0，求直线l'的方程．
双曲线C与椭圆
x2
8
+
y2
4
=1有相同的焦点，直线y=
3
x为C的一条渐近线．
（1）求双曲线C的方程；
（2）过点P（0，4）的直线l，交双曲线C于A、B两点，交x轴于Q点（Q点与C的顶点不重合），当
PQ
=λ1
QA
=λ2
QB
，且λ1+λ2=-
8
3
时，求Q点的坐标．
直线l过抛物线y2=2px（p＞0）的焦点，且交抛物线于A，B两点，交其准线于C点，已知|AF|=4，
CB
=3
BF
，则p=（　　）
A．2B．
4
3
C．
8
3
D．4
已知中心在原点的双曲线C的右焦点为（2，0），右顶点为（
3
，0）
（1）求双曲线C的方程；
（2）若直线l：y=kx+
2
与双曲线C恒有两个不同的交点A和B，且
OA
•
OB
＞2（其中O为原点）．求k的取值范围．
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率为
2
2
，其左、右焦点分别为F1，F2，点P是坐标平面内一点，且|OP|=
7
2
，
PF1
•
PF2
=
3
4
（O为坐标原点）．
（1）求椭圆C的方程；
（2）若过F1的直线L与该椭圆相交于M、N两点，且|
F1M
|=2|
F1N
|，求直线L的方程．
如图，椭圆Γ的中心在坐标原点O，过右焦点F（1，0）且垂直于椭圆对称轴的弦MN的长为3．
（1）求椭圆Γ的方程；
（2）直线l经过点O交椭圆Γ于P、Q两点，NP=NQ，求直线l的方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网