题目内容
已知F1,F2分别为椭圆C1:
+
=1(a>b>0)的上下焦点,其F1是抛物线C2:x2=4y的焦点,点M是C1与C2在第二象限的交点,且|MF2|=
.
(1)试求椭圆C1的方程;
(2)与圆x2+(y+1)2=1相切的直线l:y=k(x+t)(t≠0)交椭圆于A,B两点,若椭圆上一点P满足
+
=λ
,求实数λ的取值范围.

| x2 |
| b2 |
| y2 |
| a2 |
| 3 |
| 5 |
(1)试求椭圆C1的方程;
(2)与圆x2+(y+1)2=1相切的直线l:y=k(x+t)(t≠0)交椭圆于A,B两点,若椭圆上一点P满足
| OA |
| OB |
| OP |

(1)令M为(x0,y0),因为M在抛物线C2上,故x02=4y0,①
又|MF1|=
,则y0+1=
,②
由①②解得x0=-
,y0=
椭圆C1的两个焦点为F1(0,1),F2(0,-1),
点M在椭圆上,由椭圆定义,得
2a=|MF1|+|MF2|=
=4
∴a=2,又c=1,
∴b2=a2-c2=3
∴椭圆C1的方程为
+
=1.
(2)∵直线l:y=k(x+t)与圆x2+(y+1)2=1相切
∴
=1,即k=
(t≠0)
把y=k(x+t)代入
+
=1并整理得:
(4+3k2)x2+6k2tx+3k2t2-12=0
设A(x1,y1),B(x2,y2),则有
x1+x2=-
,y1+y2=k(x1+x2)+2kt=
∵λ
=(x1+x2,y1+y2)
∴P(
,
)
又∵点P在椭圆上
∴
+
=1
∴λ2=
=
(t≠0)
∵t2>0,∴(
)2+(
)+1>1
∴0<λ2<4
∴λ的取值范围为(-2,0)∪(0,2)
又|MF1|=
| 5 |
| 3 |
| 5 |
| 3 |
由①②解得x0=-
2
| ||
| 3 |
| 2 |
| 3 |
椭圆C1的两个焦点为F1(0,1),F2(0,-1),
点M在椭圆上,由椭圆定义,得
2a=|MF1|+|MF2|=
(-
|
∴a=2,又c=1,
∴b2=a2-c2=3
∴椭圆C1的方程为
| y2 |
| 4 |
| x2 |
| 3 |
(2)∵直线l:y=k(x+t)与圆x2+(y+1)2=1相切
∴
| |kt+1| | ||
|
| 2t |
| 1-t2 |
把y=k(x+t)代入
| y2 |
| 4 |
| x2 |
| 3 |
(4+3k2)x2+6k2tx+3k2t2-12=0
设A(x1,y1),B(x2,y2),则有
x1+x2=-
| 6k2t |
| 4+3k2 |
| 8kt |
| 4+3k2 |
∵λ
| OP |
∴P(
| -6k2t |
| (4+3k2)λ |
| 8kt |
| (4+3k2)λ |
又∵点P在椭圆上
∴
| 12k4t2 |
| (4+3k2)2λ2 |
| 16k2t2 |
| (4+3k2)2λ2 |
∴λ2=
| 4k2t2 |
| 4+3k2 |
| 4 | ||||
(
|
∵t2>0,∴(
| 1 |
| t2 |
| 1 |
| t2 |
∴0<λ2<4
∴λ的取值范围为(-2,0)∪(0,2)

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
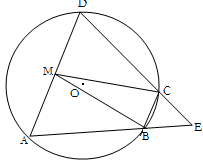
 是
是 的内接四边形,
的内接四边形,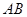 的延长线与
的延长线与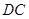 的延长线交于点
的延长线交于点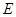 ,且
,且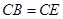 .
.
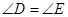 ;
;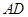 不是
不是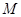 ,且
,且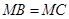 ,证明:
,证明: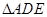 为等边三角形.
为等边三角形.
