题目内容
5.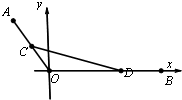 在平面直角坐标系xOy中,己知点 A(-3,4),B(9,0),C,D分别为线段OA,OB上的动点,且满足AC=BD.
在平面直角坐标系xOy中,己知点 A(-3,4),B(9,0),C,D分别为线段OA,OB上的动点,且满足AC=BD.(1)若AC=4,求直线CD的方程;
(2)证明:△OCD的外接圆恒过定点(异于原点O).
(3)当△OCD的外接圆面积为$\frac{25π}{8}$时,求△OCD的外接圆方程.
分析 (1)求出C,D的坐标,可得直线CD的斜率,即可求直线CD的方程;
(2)利用圆的一般方程,可得△OCD的外接圆的方程为x2+y2-4x-3y-5m(x+2y)=0,令x2+y2-4x-3y=0,则x+2y=0,即可得出:△OCD的外接圆恒过定点(异于原点O).
(3)当△OCD的外接圆面积为$\frac{25π}{8}$时,半径为$\frac{5\sqrt{2}}{4}$,由(2)知圆心为($\frac{5m+4}{2}$,$\frac{10m+3}{2}$),又过定点(2,-1),
求出圆的半径,建立方程求出m,即可求△OCD的外接圆方程.
解答 解:(1)因为A(-3,4),所以OA=5,
又因为AC=4,所以OC=1,所以C(-$\frac{3}{5}$,$\frac{4}{5}$),…2分
由BD=4,得D(5,0),
所以直线CD的斜率$\frac{0-\frac{4}{5}}{5-(-\frac{3}{5})}$=-$\frac{1}{7}$,…4分
所以直线CD的方程为y=-$\frac{1}{7}$(x-5),即x+7y-5=0.…5分
(2)设C(-3m,4m)(0<m≤1),则OC=5m.
所以AC=OA-OC=5-5m,
因为AC=BD,所以OD=OB-BD=5m+4,
所以D点的坐标为(5m+4,0)…6分
又设△OCD的外接圆的方程为x2+y2+Dx+Ey+F=0,
则有$\left\{\begin{array}{l}{F=0}\\{9{m}^{2}+16{m}^{2}-3mD+4mE+F=0}\\{(5m+4)^{2}+(5m+4)D+F=0}\end{array}\right.$…8分
解之得D=-(5m+4),F=0,E=-10m-3,
所以△OCD的外接圆的方程为x2+y2-4x-3y-5m(x+2y)=0,
令x2+y2-4x-3y=0,则x+2y=0,所以$\left\{\begin{array}{l}{x=0}\\{y=0}\end{array}\right.$(舍)或$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$
所以△OCD的外接圆恒过定点为(2,-1).…12分
(3)由题知外接圆面积为$\frac{25}{2}π$时半径为$\frac{5\sqrt{2}}{2}$…13分
由(2)知圆心为($\frac{5m+4}{2}$,$\frac{10m+3}{2}$),又过定点(2,-1),
故圆的半径为r=$\sqrt{(\frac{5m+4}{2}-2)^{2}+(\frac{10m+3}{2}+1)^{2}}$=$\frac{5}{2}$$\sqrt{5{m}^{2}+4m+1}$=$\frac{5\sqrt{2}}{2}$
即5m2+4m-1=0得m=-1或m=$\frac{1}{5}$
因为0<m≤1
所以m=$\frac{1}{5}$
此时所求圆方程为x2+y2-5x-5y=0…16分.
点评 本题考查圆的方程,考查外接圆恒过定点,考查待定系数法的运用,考查系数分析解决问题的能力,属于中档题.

| A. | 2,1 | B. | 2,0 | C. | 1,3 | D. | 3,1 |
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{5}$ |
| A. | $-\frac{9}{2}$ | B. | $\frac{9}{2}$ | C. | $\frac{1}{4}$ | D. | -4 |
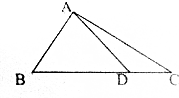 已知在△ABC中,点D在BC上,且满足$\overrightarrow{BD}$=3$\overrightarrow{DC}$,若$\overrightarrow{AD}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,则x+y=1.
已知在△ABC中,点D在BC上,且满足$\overrightarrow{BD}$=3$\overrightarrow{DC}$,若$\overrightarrow{AD}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,则x+y=1. 海上某货轮在A处看灯塔B在货轮的北偏东75°,距离为12$\sqrt{6}$海里;在A处看灯塔C在货轮的北偏西30°,距离为8$\sqrt{3}$海里;货轮向正北由A处行驶到D处时看灯塔B在货轮的北偏东120°.
海上某货轮在A处看灯塔B在货轮的北偏东75°,距离为12$\sqrt{6}$海里;在A处看灯塔C在货轮的北偏西30°,距离为8$\sqrt{3}$海里;货轮向正北由A处行驶到D处时看灯塔B在货轮的北偏东120°.