题目内容
设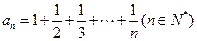 ,是否存在整式
,是否存在整式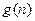 ,使得
,使得
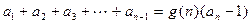 对n≥2的一切自然数都成立?并试用数学
对n≥2的一切自然数都成立?并试用数学
归纳法证明你的结论.
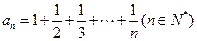 ,是否存在整式
,是否存在整式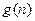 ,使得
,使得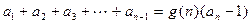 对n≥2的一切自然数都成立?并试用数学
对n≥2的一切自然数都成立?并试用数学归纳法证明你的结论.
解:假设存在整式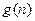 ,使得
,使得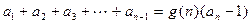 对n≥2的一切自然数都成立,则
对n≥2的一切自然数都成立,则
当n=2时有 ,又∵
,又∵ ,∴
,∴ ;
;
当n=3时有 ,又∵
,又∵ ,
,
∴ ;……, 猜想:g(n)=n(n≥2),
;……, 猜想:g(n)=n(n≥2),
下面用数学归纳法加以证明:
(1)当n=2时,已经得到证明.
(2)假设当n=k(k≥2,k∈N)时,结论成立,即
存在g(k)=k,使得 对k≥2的一切自然数都成立成立.则当n=k+1时,
对k≥2的一切自然数都成立成立.则当n=k+1时,


 ,
,
又∵ ∴
∴ ,
,
∴
 ,
,
∴当n=k+1时,命题成立.
由(1)(2)知,对一切n(n≥2,n∈N*)有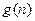 =n,使得
=n,使得
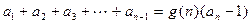 都成立.
都成立.
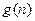 ,使得
,使得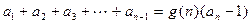 对n≥2的一切自然数都成立,则
对n≥2的一切自然数都成立,则当n=2时有
 ,又∵
,又∵ ,∴
,∴ ;
;当n=3时有
 ,又∵
,又∵ ,
,∴
 ;……, 猜想:g(n)=n(n≥2),
;……, 猜想:g(n)=n(n≥2),下面用数学归纳法加以证明:
(1)当n=2时,已经得到证明.
(2)假设当n=k(k≥2,k∈N)时,结论成立,即
存在g(k)=k,使得
 对k≥2的一切自然数都成立成立.则当n=k+1时,
对k≥2的一切自然数都成立成立.则当n=k+1时,

 ,
,又∵
 ∴
∴ ,
,∴

 ,
,∴当n=k+1时,命题成立.
由(1)(2)知,对一切n(n≥2,n∈N*)有
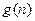 =n,使得
=n,使得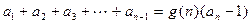 都成立.
都成立.略

练习册系列答案
相关题目
 ,且
,且 ,求证:
,求证:
 ,求证
,求证
 ≥
≥ >0,求证:
>0,求证: ≥
≥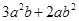
 (
( )的数列
)的数列 是等比数列.”的大前提是
是等比数列.”的大前提是 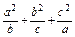 ≥a+b+c.
≥a+b+c. ,
, ,并且对于任意
,并且对于任意 ,
, 成立. 猜想
成立. 猜想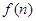 的表达式为
的表达式为



 个圆圈,每个图案中圆圈的总数是
个圆圈,每个图案中圆圈的总数是 ,按此规律推出:当
,按此规律推出:当 时,
时, 的关系式 .
的关系式 .


