题目内容
【题目】(1)求函数
取得最大值时的自变量
的集合并说出最大值；
(2)求函数
的单调递增区间.
【答案】（1）3；（2）
和
.
【解析】
(1)根据余弦函数的值域可求出函数
的最大值，由
，可求得 取得最大值时自变量
的集合；（2）由
，求得的范围，可得函数
的增区间，再结合
，进一步确定函数的增区间.
(1)由2x = + 2k, 得x =
+ k, k Z.
所以, 函数y = - 3cos2x, x R取得最大值时的自变量x的集合是{x | x 
+ k, k Z}.
函数y = - 3cos2x, x R的得最大值是3.
(2)由-+ 2k 2x +
+ 2k, 得-
+ k x 
+ k, k Z.
设A = [0, ], B = {x |-+ k x + k, k Z}, 易知A∩B = [0,]∪[
, ]. 所以, 函数y = 3sin(2x +), x [0, ]的单调递增区间为[0,]和[, ].
练习册系列答案
相关题目
【题目】某学校有120名教师，且年龄都在20岁到60岁之间，各年龄段人数按分组，其频率分布直方图如图所示，学校要求每名教师都要参加两项培训，培训结束后进行结业考试．已知各年龄段两项培训结业考试成绩优秀的人数如表示，假设两项培训是相互独立的，结业考试成绩也互不影响．
年龄分组 | A项培训成绩优秀人数 | B项培训成绩优秀人数 |
[20，30） | 30 | 18 |
[30，40） | 36 | 24 |
[40，50） | 12 | 9 |
[50，60] | 4 | 3 |
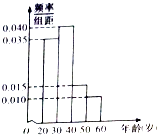
（1）若用分层抽样法从全校教师中抽取一个容量为40的样本，求从年龄段[20，30）抽取的人数；
（2）求全校教师的平均年龄；
（3）随机从年龄段[20，30）和[30，40）内各抽取1人，设这两人中两项培训结业考试成绩都优秀的人数为X，求X的概率分布和数学期望．
