题目内容
【题目】如图,已知抛物线C:y2=4x,过焦点F斜率大于零的直线l交抛物线于A、B两点,且与其准线交于点D.
(Ⅰ)若线段AB的长为5,求直线l的方程;
(Ⅱ)在C上是否存在点M,使得对任意直线l,直线MA,MD,MB的斜率始终成等差数列,若存在求点M的坐标;若不存在,请说明理由.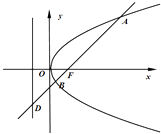
【答案】解:(Ⅰ)焦点F(1,0)
∵直线l的斜率不为0,所以设l:x=my+1,
A(x1 , y1),B(x2 , y2)
由 ![]() 得y2﹣4my﹣4=0,
得y2﹣4my﹣4=0,
y1+y2=4m,y1y2=﹣4,![]() ,
,![]() ,
,
∴ ![]() ,
,
∴ ![]() .
.
∴直线l的斜率k2=4,
∵k>0,∴k=2,
∴直线l的方程为2x﹣y﹣2=0.
(Ⅱ)设M(a2 , 2a),
kMA= ![]() =
= ![]() ,
,
同理,kMB= ![]() ,kMD=
,kMD=  ,
,
∵直线MA,MD,MB的斜率始终成等差数列,
∴2  =
= ![]() +
+ ![]() 恒成立;
恒成立;
∴ ![]() =
= ![]() ,
,
又∵y1+y2=4m,y1y2=﹣4,
∴(a2﹣1)(m+ ![]() )=0,
)=0,
∴a=±1,
∴存在点M(1,2)或M(1,﹣2),使得对任意直线l,
直线MA,MD,MB的斜率始终成等差数列.
【解析】(Ⅰ)设l:x=my+1,A(x1 , y1),B(x2 , y2),则联立方程化简可得y2﹣4my﹣4=0,从而可得 ![]() ,从而求直线l的方程;
,从而求直线l的方程;
(Ⅱ)设M(a2 , 2a),则kMA= ![]() =
= ![]() ,kMB=
,kMB= ![]() ,kMD=
,kMD= ![]() ,则
,则 ![]() =
= ![]() ,从而可得(a2﹣1)(m+
,从而可得(a2﹣1)(m+ ![]() )=0,从而求出点M的坐标.
)=0,从而求出点M的坐标.
【考点精析】利用一般式方程对题目进行判断即可得到答案,需要熟知直线的一般式方程:关于![]() 的二元一次方程
的二元一次方程![]() (A,B不同时为0).
(A,B不同时为0).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目