题目内容
【题目】已知函数![]() .
.
(1)若曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,求a,b的值;
,求a,b的值;
(2)如果![]() 是函数
是函数![]() 的两个零点,
的两个零点, ![]() 为函数
为函数![]() 的导数,证明:
的导数,证明: ![]()
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】试题分析:
(1)由曲线![]() 在点
在点![]() 处的切线方程,可求出切线斜率,即为函数
处的切线方程,可求出切线斜率,即为函数![]() 在x=1处的导数,由此可求出
在x=1处的导数,由此可求出![]() ,再求出
,再求出![]() ,即得点
,即得点![]() ,再将点
,再将点![]() 切线方程为
切线方程为![]() ,即可求出
,即可求出![]() .
.
(2)先求出![]() ,再由
,再由![]() 是函数
是函数![]() 的两个零点这一条件,将
的两个零点这一条件,将![]() 转为
转为![]() 的数学表达式,再通过换元
的数学表达式,再通过换元![]() ,得到了
,得到了![]() 与一个变量
与一个变量![]() 的关系,最终将问题转化为求函数的单调性与最值问题。
的关系,最终将问题转化为求函数的单调性与最值问题。
试题解析:
(1)由切线方程为![]() ,可知斜率
,可知斜率![]() , 而
, 而![]() .所以
.所以![]() ,得
,得![]() ,由此
,由此![]() .
.
而![]() ,所以
,所以![]() ,
, ![]() ,得
,得![]() .
.
(2)因为, ![]() ,所以
,所以![]()
![]() 是函数
是函数![]() 的两个零点
的两个零点 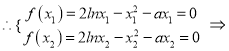
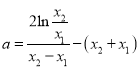 ,
,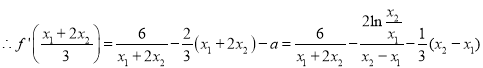
![]() ,
,
故要证![]() ,
,
![]() 只需证
只需证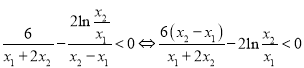
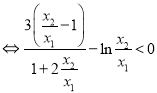
,令![]() 则设
则设![]() 下面证
下面证![]()
![]()
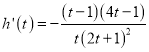
![]() 恒成立
恒成立
![]() 在
在![]() 单调递减,
单调递减, ![]() 即
即![]()

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案
相关题目