题目内容
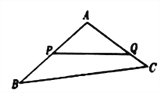
【题目】如图，某生态园将一块三角形地
的一角
开辟为水果园，已知角
为
， 
的长度均大于200米，现在边界
处建围墙，在
处围竹篱笆.
（1）若围墙
、
总长度为200米，如何可使得三角形地块
面积最大？
（2）已知竹篱笆长为
米， 
段围墙高1米， 
段围墙高2米，造价均为每平方米100元，求围墙总造价的取值范围.
【答案】（1）
(米)时， 
；（2）围墙总造价的取值范围为
(元).
【解析】试题分析：（1）根据正弦定理求得
，然后用基本不等式求解；（2）由正弦定理求得
，故围墙总造价
，根据
的范围求得y的取值范围即可。
试题解析：（1）设
(米)，则
,所以
(米2)
当且仅当
时，取等号。即
(米)， 
(米2).
(2)由正弦定理
，
得
故围墙总造价
因为
， 
所以
.
答：围墙总造价的取值范围为
(元).
练习册系列答案
相关题目
