题目内容
【题目】已知a≥2,不等式logax+loga[(a+1)ak-1-x]≥2k-1的解集为A,其中a∈N*,k∈N.
(1)求A.
(2)设f(k)表示A中自然数个数,求和Sn=f(1)+f(2)+…+f(n).
(3)当a=2时,比较Sn与n2+n的大小,并证明你的结论.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)见解析
;(3)见解析
【解析】分析:(1)利用对数函数的单调性,转化为不等式组,解之即可;
(2)由(1)明确f(k)表示A中自然数个数,累加求和即可;
(3)先用特例猜想二者大小,然后用数学归纳法证明.
详解:(1)不等式同解于
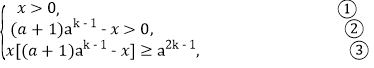 ,
,
由③,得x2-(a+1)ak-1x+a2k-1≤0.
∵a≥2,∴ak-1<ak.
∴ak-1≤x≤ak,且该式满足①,②.
∴A={x|ak-1≤x≤ak}.
(2)由题意知f(k)=ak-ak-1+1,Sn=(a-a0+1)+(a2-a+1)+…+(an-an-1+1)=an+n-1.
(3)当a=2时,Sn=2n+n-1,Sn-(n2+n)=2n-n2-1.
当n=1时,S1=12+1;
当n=2时,S2<22+2;
当n=3时,S3<32+3;
当n=4时,S4<42+4;
当n=5时,S5>52+5.
猜想当n≥5(n∈N)时,Sn>n2+n.
下面用数学归纳法证明:
①当n=5时,已验证.
②假设当n=k(k≥5)时,Sk>k2+k成立,即2k>k2+1成立,则当n=k+1时,Sk+1-[(k+1)2+(k+1)]=2k+1-(k+1)2-1=2×2k-k2-2k-2>2(k2+1)-k2-2k-2=k2-2k=k(k-2)>0,即Sk+1>[(k+1)2+(k+1)],∴当n=k+1时结论成立.
根据①②可知,对任何n≥5(n∈N*),都有Sn>n2+n成立.
综上所述,当n=1时,Sn=n2+n;当n=2,3,4时,Sn<n2+n;当n≥5(n∈N*)时,Sn>n2+n.

 名校课堂系列答案
名校课堂系列答案【题目】由国家公安部提出,国家质量监督检验检疫总局发布的《车辆驾驶人员血液、呼气酒精含量阀值与检验标准(![]() )》于
)》于![]() 年
年![]() 月
月![]() 日正式实施.车辆驾驶人员酒饮后或者醉酒后驾车血液中的酒精含量阀值见表.经过反复试验,一般情况下,某人喝一瓶啤酒后酒精在人体血液中的变化规律的“散点图”见图,
日正式实施.车辆驾驶人员酒饮后或者醉酒后驾车血液中的酒精含量阀值见表.经过反复试验,一般情况下,某人喝一瓶啤酒后酒精在人体血液中的变化规律的“散点图”见图,

喝![]() 瓶啤酒的情况
瓶啤酒的情况
且图表示的函数模型 ,则该人喝一瓶啤酒后至少经过多长时间才可以驾车(时间以整小时计算)?(参考数据:
,则该人喝一瓶啤酒后至少经过多长时间才可以驾车(时间以整小时计算)?(参考数据:![]() ,
,![]() )
)
( )
驾驶行为类型 | 阀值 |
饮酒后驾车 |
|
醉酒后驾车 |
|
车辆驾车人员血液酒精含量阀值
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【题目】甲、乙两家外卖公司,其送餐员的日工资方案如下:甲公司的底薪70元,每单抽成4元;乙公司无底薪,40单以内(含40单)的部分每单抽成5元,超出40单的部分每单抽成7元,假设同一公司送餐员一天的送餐单数相同,现从两家公司各随机抽取一名送餐员,并分别记录其100天的送餐单数,得到如表频数表: 甲公司送餐员送餐单数频数表
送餐单数 | 38 | 39 | 40 | 41 | 42 |
天数 | 20 | 40 | 20 | 10 | 10 |
乙公司送餐员送餐单数频数表
送餐单数 | 38 | 39 | 40 | 41 | 42 |
天数 | 10 | 20 | 20 | 40 | 10 |
(Ⅰ)现从甲公司记录的100天中随机抽取两天,求这两天送餐单数都大于40的概率;
(Ⅱ)若将频率视为概率,回答下列问题:
(i)记乙公司送餐员日工资为X(单位:元),求X的分布列和数学期望;
(ii)小明拟到甲、乙两家公司中的一家应聘送餐员,如果仅从日工资的角度考虑,请利用所学的统计学知识为他作出选择,并说明理由.