题目内容
【题目】已知E，F分别为正方体ABCD﹣A1B1C1D的棱AB，AA1上的点，且AE=
AB，AF=
AA1 ， M，N分别为线段D1E和线段C1F上的点，则与平面ABCD平行的直线MN有（ ）
A.1条
B.3条
C.6条
D.无数条
【答案】D
【解析】解：取BH=
BB1 ， 连接FH，则FH∥C1D
连接HE，在D1E上任取一点M，
过M在面D1HE中，作MG∥HO，交D1H于G，
其中O为线段OE=D1E
再过G作GN∥FH，交C1F于N，连接MN，
由于GM∥HO，HO∥KB，KB平面ABCD，
GM平面ABCD，
所以GM∥平面ABCD，
同理由NG∥FH，可推得NG∥平面ABCD，
由面面平行的判定定理得，平面MNG∥平面ABCD，
则MN∥平面ABCD．
由于M为D1E上任一点，故这样的直线MN有无数条．
故选D．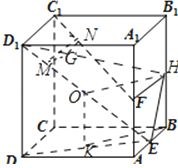
【考点精析】通过灵活运用直线与平面平行的性质，掌握一条直线与一个平面平行，则过这条直线的任一平面与此平面的交线与该直线平行;简记为：线面平行则线线平行即可以解答此题．
学练快车道快乐假期暑假作业新疆人民出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
小学暑假作业东南大学出版社系列答案
【题目】某校100名学生期中考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：[50，60），[60，70），[70，80），[80，90），[90，100]．
（1）求图中
的值；
（2）根据频率分布直方图，估计这100名学生语文成绩的平均分，众数，中位数；
（3）若这100名学生语文成绩某些分数段的人数（
）与数学成绩相应分数段的人数（
）之比如下表所示，求数学成绩在[50，90）之外的人数．
分数段 | [50，60） | [60，70） | [70，80） | [80，90） |
| 1：1 | 2：1 | 3：4 | 4：5 |
【题目】某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系，他们分别到气象局与某医院抄录了1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数，得到如下资料：
日期 | 1月10日 | 2月10日 | 3月10日 | 4月10日 | 5月10日 | 6月10日 |
昼夜温差 | 10 | 11 | 13 | 12 | 8 | 6 |
就诊人数 | 22 | 25 | 29 | 26 | 16 | 12 |
该兴趣小组确定的研究方案是：先从这六组数据中选取2组，用剩下的4组数据求线性回归方程，再用被选取的2组数据进行检验．
（Ⅰ）若选取的是1月与6月的两组数据，请根据2月至5月份的数据，求出y关于x的线性回归方程
＝
x＋
；
（Ⅱ）若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人，则认为得到的线性回归方程是理想的，试问该小组所得线性回归方程是否理想．
附：
（参考数据
）
