题目内容
【题目】△ABC，满足bcosC+ 
bsinC﹣a﹣c=0
（1）求角B的值；
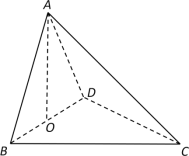
（2）若a=2，且AC边上的中线BD长为 
，求△ABC的面积．
【答案】
（1）解：由已知条件得： 
∴ 
即 
．
∵sinC＞0得 
，∴ 
又 
，∴ 
，∴ 
（2）解：由已知得： 
+ 
=2 
，平方得： 2+ 2+2 =4 2，
即c2+a2+2cacos 
=84，
又a=2，∴c2+2c﹣80=0
解得：c=8或c=﹣2（舍去）
∴S△ABC= 
﹣ 
=4 
．
【解析】（1）由已知条件，利用正弦定理，结合辅助角公式，即可求角B的值；（2）若a=2，且AC边上的中线BD长为 
，建立关于c的方程，利用三角形的面积公式求△ABC的面积．
【考点精析】根据题目的已知条件，利用余弦定理的定义的相关知识可以得到问题的答案，需要掌握余弦定理:
;
;
．
练习册系列答案
巧学巧练系列答案
课课练江苏系列答案
相关题目
【题目】某公司的管理者通过公司近年来科研费用支出x(百万元)与公司所获得利润y(百万元)的散点图发现，y与x之间具有线性相关关系，具体数据如下表：
年份 | 2010 | 2011 | 2012 | 2013 | 2014 |
科研费用x(百万元) | 1.6 | 1.7 | 1.8 | 1.9 | 2.0 |
公司所获利润y(百万元) | 1 | 1.5 | 2 | 2.5 | 3 |
(1)求y关于x的回归直线方程；
(2)若该公司的科研投入从2011年开始连续10年每一年都比上一年增加10万元，预测2017年该公司可获得的利润约为多少万元．