题目内容
【题目】已知椭圆C: ![]() +
+ ![]() =1(a>b>0)的左顶点为(﹣2,0),离心率为
=1(a>b>0)的左顶点为(﹣2,0),离心率为 ![]() .
. 
(1)求椭圆C的方程;
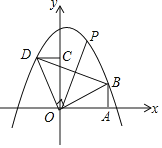
(2)已知直线l过点S(4,0),与椭圆C交于P,Q两点,点P关于x轴的对称点为P′,P′与Q两点的连线交x轴于点T,当△PQT的面积最大时,求直线l的方程.
【答案】
(1)解:由题意可得 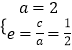 ,可得c=1,b=
,可得c=1,b= ![]() =
= ![]() .
.
即有椭圆的方程为 ![]() +
+ ![]() =1;
=1;
(2)解:设直线l的方程为x=my+4,P(x1,y1),Q(x2,y2),则P'(x1,﹣y1),
联立 ![]() 得(4+3m2)y2+24my+36=0,
得(4+3m2)y2+24my+36=0,
则△=(24m)2﹣144(4+3m2)=144(m2﹣4)>0,即m2>4.
又y1+y2=﹣ ![]() ,y1y2=
,y1y2= ![]() ,
,
直线PQ的方程为y= ![]() (x﹣x1)﹣y1
(x﹣x1)﹣y1
则xT= ![]() =
= ![]()
= ![]() =
= ![]() +4=1,
+4=1,
则T(1,0),故|ST|=3
所以S△PQT=S△SQT﹣S△SPT= ![]() |y1﹣y2|=
|y1﹣y2|= ![]()
![]() =
= ![]() ,
,
令t= ![]() >0,
>0,
则S△PQT= ![]() =
= ![]() ≤
≤ ![]() =
= ![]() ,
,
当且仅当t2= ![]() 即m2=
即m2= ![]() 即m=±
即m=± ![]() 时取到“=”,
时取到“=”,
故所求直线l的方程为x=± ![]() y+4.
y+4.
【解析】(1)运用椭圆的离心率公式和顶点坐标,以及a,b,c的关系,解得a,b,进而得到椭圆方程;(2)设直线l的方程为x=my+4,P(x1 , y1),Q(x2 , y2),则P'(x1 , ﹣y1),联立直线和椭圆方程,运用韦达定理和判别式大于0,求得直线PQ的方程,令y=0,可得T的横坐标,化简可得T(1,0),由S△PQT=S△SQT﹣S△SPT= ![]() |y1﹣y2|,运用韦达定理,由换元法化简整理运用基本不等式可得最大值,以及此时直线的方程.
|y1﹣y2|,运用韦达定理,由换元法化简整理运用基本不等式可得最大值,以及此时直线的方程.
【考点精析】本题主要考查了椭圆的标准方程的相关知识点,需要掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() 才能正确解答此题.
才能正确解答此题.

 阅读快车系列答案
阅读快车系列答案【题目】某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
保费 | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:
出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
频数 | 60 | 50 | 30 | 30 | 20 | 10 |
(1)记A为事件:“一续保人本年度的保费不高于基本保费”,求P(A)的估计值;
(2)记B为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的160%”,求P(B)的估计值;
(3)求续保人本年度平均保费的估计值.