äãá¢áÖàï
Àƒäãá¢À¢á°¿¨ùƒçá¿ÉâÚíÔë´¿»¿¨ùƒ§■áõâÇ¢óîÅñîÆûøÏ°—x(¯ìë·åˆ)ÆŠ¿¨ùƒùª£þçûâ«àµy(¯ìë·åˆ)çáèÂçÐë¥ñÂüøȘyÆŠxøÛ¥ðƒÔÆÅüÔÅåüÁ¿Ä¿ÄüçȘƒÔäÍò»ƒïàÓüôÝÚȤ
áõñï | 2010 | 2011 | 2012 | 2013 | 2014 |
¢óîÅñîÆûx(¯ìë·åˆ) | 1.6 | 1.7 | 1.8 | 1.9 | 2.0 |
¿¨ùƒùª£þâ«àµy(¯ìë·åˆ) | 1 | 1.5 | 2 | 2.5 | 3 |
(1)úµy¿ÄÆÖxçá£Ä¿ÕøÝüÔñ§°äÈ£
(2)ඡû¿¨ùƒçá¢óîÅëÑàŠÇÆ2011áõ¢ˆò¥ê˜Å½10áõû¢Ø£áõÑ¥ÝàèüØ£áõå—¥Æ10ë·åˆÈ˜åÊýã2017áõ¡û¿¨ùƒ¢è£þçûçáâ«àµå¥öˆÑÁèìë·åˆÈÛ
ÀƒÇÞ¯¡À¢È´1Èˋ![]() ȣȴ2Èˋ4.5(¯ìë·åˆ)
ȣȴ2Èˋ4.5(¯ìë·åˆ)
Àƒ§ãö—À¢
Â顪ƒïÝÚøÅò»ƒïȘ¥óùа—![]() Ș
Ș![]() Șúµ°—£Ä¿Õüçò»È˜ÅÇ°—£Ä¿ÕøÝüÔñ§°ä
Șúµ°—£Ä¿Õüçò»È˜ÅÇ°—£Ä¿ÕøÝüÔñ§°ä
ÂóÆèäãøˆ![]() áõòÝ¢óîÅëÑàŠöˆ
áõòÝ¢óîÅëÑàŠöˆ![]() ¯ìë·åˆÈ˜ÇºàŠ£Ä¿Õñ§°ä¥Ç¢èúµçû§Ã¿«
¯ìë·åˆÈ˜ÇºàŠ£Ä¿Õñ§°ä¥Ç¢èúµçû§Ã¿«
(1)ƒÙ¥óùТèçû
![]() ȧ1.8Ș
ȧ1.8Ș![]() ȧ2Ș
ȧ2Ș![]() ȧ18.5Ș
ȧ18.5Ș
![]() ȧ
ȧ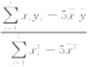 ȧ
ȧ![]() ȧ5Ș
ȧ5Ș
![]() ȧ
ȧ![]() ÈÙ
ÈÙ![]()
![]() ȧ2ÈÙ5Àê1.8ȧÈÙ7.
ȧ2ÈÙ5Àê1.8ȧÈÙ7.
¿òùªúµçá£Ä¿ÕøÝüÔñ§°äöˆ![]() ȧ5xÈÙ7.
ȧ5xÈÙ7.
(2)Æèäã¢èøˆç§2017áõòÝ¢óîÅëÑàŠöˆ2.3¯ìë·åˆÈ˜¿ò¢èåÊýã¡û¿¨ùƒùª£þçûçáâ«àµå¥öˆ5Àê2.3ÈÙ7ȧ4.5(¯ìë·åˆ)ÈÛ

Àƒäãá¢À¢á°øÅîÏç¼ýÕêùá°¯Áà¨ý¢45û«ë˜îÏýö¥ÆòÕñ´èÓëé¤ëîï§ýèÓëéçáúÕ¢—Șò»ƒïàÓüôÝÚȤȴçËö£È¤àùÈˋ
ýö¥ÆòÕñ´èÓëé | öÇýö¥ÆòÕñ´èÓëé | |
ýö¥Æîï§ýèÓëé | 8 | 5 |
öÇýö¥Æîï§ýèÓëé | 2 | 30 |
È´1ÈˋÇÆ¡û¯ÁùÌ£ºîÀ1û«ë˜îÏȘúµ¡ûë˜îÏøêèìýö¥ÆØ£¡—èÓëéçá¡éôòÈ£
È´2ÈˋåÖ¥àýö¥ÆòÕñ´èÓëéÆøýö¥Æîï§ýèÓëéçá8û«ë˜îÏøÅȘÆÅ5û«áÅë˜îÏA1ȘA2ȘA3ȘA4ȘA5Ș3û«éÛë˜îÏB1ȘB2ȘB3ÈÛüøÇÆíã5û«áÅë˜îϤë3û«éÛë˜îÏøÅ¡¼ùÌ£ºîÀ1àùȘúµA1Ý£îÀøÅúØB1öÇÝ£îÀøÅçá¡éôòÈÛ
Àƒäãá¢À¢á°üíøøçᣪ݃ÝÈñîöˆa(çËö£È¤åˆ)Ș¥äŽ¿¤ô·¡ûüíøøçáëÑÝÈàù°óöˆÅ½ÝÈàùȘŽÝÈàù݃áõÑàçáÝÈñîÆŠóðèüáõÑà°—üíÇöò»çá¿ÄêˆàÓüôȤ
èüáõÑà°—üíÇöò» | 0 | 1 | 2 | 3 | 4 | Àï5 |
ÝÈñî | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
ùÌ£ºç¼ýÕêù¡ûüíøøçá200û«Å½ÝÈàùåÖØ£áõáÖçá°—üíúÕ¢—Șçûç§àÓüôë°¥óÝÚȤ
°—üíÇöò» | 0 | 1 | 2 | 3 | 4 | Àï5 |
óçò» | 60 | 50 | 30 | 30 | 20 | 10 |
(1)¥úAöˆòô¥±È¤À¯Ø£Å½ÝÈàù݃áõÑàçáÝÈñîý£¡ÔÆÖ£ªÝƒÝÈñîÀÝȘúµP(A)çá¿â¥óøçÈ£
(2)¥úBöˆòô¥±È¤À¯Ø£Å½ÝÈàù݃áõÑàçáÝÈñî¡ÔÆÖ£ªÝƒÝÈñîç¨ý£¡ÔÆÖ£ªÝƒÝÈñîçá160%ÀÝȘúµP(B)çá¿â¥óøçÈ£
(3)úµÅ½ÝÈàù݃áõÑà󧃪ÝÈñîçá¿â¥óøçÈÛ