题目内容
【题目】如图,在四棱锥![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,底面
,底面![]() 为长方形,且
为长方形,且![]() ,
,![]() 是
是![]() 的中点,作
的中点,作![]() 交
交![]() 于点
于点![]() .
.

(1)证明:![]() 平面
平面![]() ;
;
(2)若三棱锥![]() 的体积为
的体积为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)在(2)的条件下,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】分析:(1)推导出![]() ,
,![]() ,从而
,从而![]() 平面
平面![]() ,进而
,进而![]() ,再证出
,再证出![]() ,从而
,从而![]() 平面
平面![]() ,
,![]() ,再由
,再由![]() ,能证明
,能证明![]() 平面
平面![]() .
.
(2)由![]() 两两垂直,以
两两垂直,以![]() 为坐标原点,建立空间直角坐标系
为坐标原点,建立空间直角坐标系![]() ,利用向量法能求出直线
,利用向量法能求出直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(3)求出平面![]() 的法向量和平面PBC的法向量,利用向量法能求出二面角D-BP-C的余弦值.
的法向量和平面PBC的法向量,利用向量法能求出二面角D-BP-C的余弦值.
详解:
(1)证明:∵![]() 底面
底面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() ,
,
由于底面![]() 为长方形,∴
为长方形,∴![]() ,而
,而![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,∴
,∴![]() ,
,
∵![]() ,
,![]() 为
为![]() 的中点,∴
的中点,∴![]() ,
,
∵![]() ,∴
,∴![]() 平面
平面![]() ,
,
∴![]() ,又
,又![]() ,
,![]() ,
,
∴![]() 平面
平面![]() .
.
(2)由题意易知![]() 两两垂直,以
两两垂直,以![]() 为坐标原点,建立如图空间直角坐标系
为坐标原点,建立如图空间直角坐标系![]() ,可得
,可得![]() ,
,
设![]() ,则有
,则有![]() ,∴
,∴![]()
∴![]() ,
,
∴![]() ,
,![]()
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,且由(1)知
,且由(1)知![]() 为平面
为平面![]() 的法向量
的法向量
∴![]()
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
(3)由(2)知![]() ,
,![]() ,
,![]()
设平面![]() 的法向量
的法向量![]() ,由
,由![]() ,则
,则![]()
令![]() ,则
,则![]() ,
,
∴![]()
由(1)![]() 平面
平面![]() ,
,
∴![]() 为平面PBC的法向量,
为平面PBC的法向量,![]()
设二面角![]() 为
为![]() ,则
,则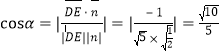
所以二面角![]() 的余弦值为
的余弦值为![]() .
.

【题目】某企业有甲、乙两套设备生产同一种产品,为了检测两套设备的生产质量情况,随机从两套设备生产的大量产品中各随机抽取了100件产品作为样本来检测一项质量指标值,若产品的该项质量指标值落在![]() 内,则为合格品,否则为不合格品.表1是甲套设备的样本的频数分布表,图是乙套设备的样本的频率分布直方图.
内,则为合格品,否则为不合格品.表1是甲套设备的样本的频数分布表,图是乙套设备的样本的频率分布直方图.

表甲套设备的样本的频数分布表
质量指标值 |
|
|
|
|
|
|
频数 | 2 | 10 | 36 | 38 | 12 | 2 |
(1)将频率视为概率.若乙套设备生产了10000件产品,则其中的合格品约有多少件?
(2)填写下面的2×2列联表,并判断能否在犯错误的概率不超过0.01的前提下,认为该企业生产的这种产品的质量指标值与甲、乙两套设备的选择有关.
甲套设备 | 乙套设备 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
附表及公式: ,其中
,其中![]() ;
;
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】手机厂商推出一款6寸大屏手机,现对500名该手机使用者(200名女性,300名男性)进行调查,对手机进行评分,评分的频数分布表如下:
女性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
频数 | 20 | 40 | 80 | 50 | 10 | |
男性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
频数 | 45 | 75 | 90 | 60 | 30 |
(1)完成下列频率分布直方图,并比较女性用户和男性用户评分的波动大小(不计算具体值,给出结论即可);

(2)把评分不低于70分的用户称为“评分良好用户”,能否有![]() 的把握认为“评分良好用户”与性别有关?
的把握认为“评分良好用户”与性别有关?
参考附表:
|
|
|
|
|
|
|
|
|
|
参考公式 ,其中
,其中![]()


