题目内容
16.记集合$A=\left\{(x,y)|{x}^{2}+{y}^{2}≤1\right\},B=\{(x,y)|\left\{\begin{array}{l}x+y≤1\\ x≥0\\ y≥0\end{array}\right.\}$,构成的平面区域分别为M,N,现随机地向M中抛一粒豆子(大小忽略不计),则该豆子落入N中的概率为$\frac{1}{2π}$.分析 平面区域M、N,分别为圆与直角三角形,面积分别为π,$\frac{1}{2}$,利用几何概型的概率公式解之即可.
解答 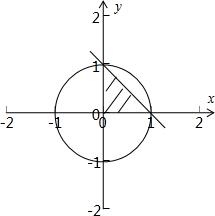 解:集合$A=\{(x,y)|{x}^{2}+{y}^{2}≤1\},B=\left\{(x,y)|\left\{\begin{array}{l}x+y≤1\\ x≥0\\ y≥0\end{array}\right\}$构成的平面区域M、N,分别为圆与直角三角形,
解:集合$A=\{(x,y)|{x}^{2}+{y}^{2}≤1\},B=\left\{(x,y)|\left\{\begin{array}{l}x+y≤1\\ x≥0\\ y≥0\end{array}\right\}$构成的平面区域M、N,分别为圆与直角三角形,
面积分别为π,$\frac{1}{2}$,随机地向M中抛一粒豆子(大小忽略不计),则该豆子落入N中的概率为$\frac{\frac{1}{2}}{π}$=$\frac{1}{2π}$.
答案为:$\frac{1}{2π}$.
点评 本题主要考查了几何概型的概率,确定区域面积是关键,属于中档题.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
6.已知a>b>0,则下列不等关系式中正确的是( )
| A. | sina>sinb | B. | log2a<log2b | C. | a${\;}^{\frac{1}{2}}$<b${\;}^{\frac{1}{2}}$ | D. | ($\frac{1}{3}$)a<($\frac{1}{3}$)b |
7.”直线与抛物线相切”是“直线与抛物线只有一个公共点”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 非充分非必要条件 |
5.若x,y∈R,则x>y的一个充分不必要条件是( )
| A. | |x|>|y| | B. | x2>y2 | C. | $\sqrt{x}>\sqrt{y}$ | D. | x3>y3 |
 已知函数$f(x)=Asin(ωx+\frac{π}{6})$(A>0,ω>0)的部分图象如图所示,其中M$(-\frac{1}{6},0)$为图象与x轴的交点,$P(\frac{1}{3},2)$为图象的最高点.
已知函数$f(x)=Asin(ωx+\frac{π}{6})$(A>0,ω>0)的部分图象如图所示,其中M$(-\frac{1}{6},0)$为图象与x轴的交点,$P(\frac{1}{3},2)$为图象的最高点.